目录：
分类与回归树（Classification and Regression Trees, CART） 是由四人帮Leo Breiman, Jerome Friedman, Richard Olshen与Charles Stone于1984年提出，既可用于分类也可用于回归。本文将主要介绍用于分类的CART。CART 被称为数据挖掘领域内里程碑式的算法。
不同于C4.5，CART本质是对特征空间进行二元划分（即CART 生成的决策树是一棵二叉树），并能够对标量属性（nominal attribute）与连续属性（continuous attribute）进行分裂。
决策树生成涉及到两个问题：如何选择最优特征属性进行分裂，以及停止分裂的条件是什么。
CART 对特征属性进行二元分裂。特别地，当特征属性为标量或连续时，可选择如下方式分裂：样本记录满足条件则分裂给左子树，否则则分裂给右子树。
标量属性
进行分裂的条件可置为不等于属性的某值；比如，标量属性Car Type取值空间为{Sports, Family, Luxury}，二元分裂与多路分裂如下:
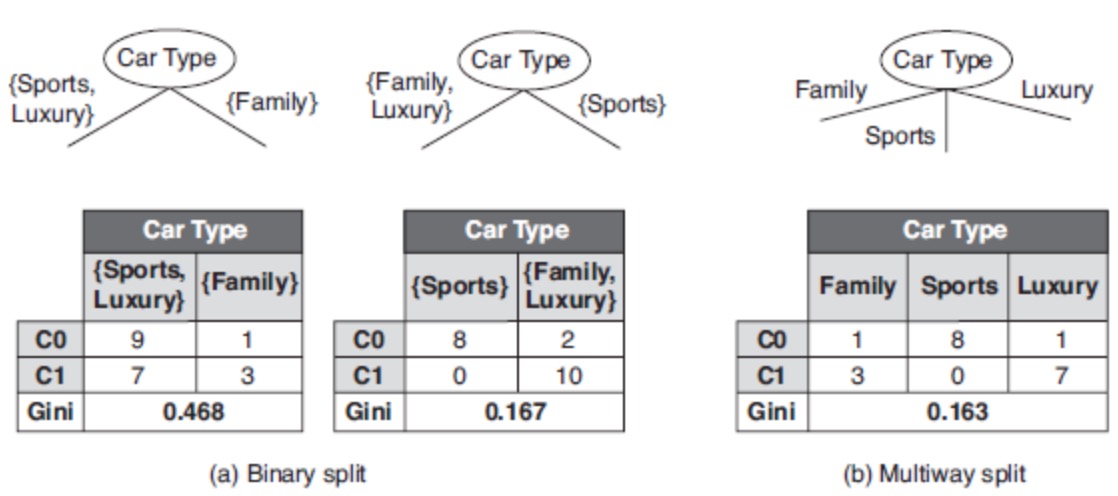
连续属性
条件可置为不大于ε；比如，连续属性Annual Income，ε取属性相邻值的平均值，其二元分裂结果如下：
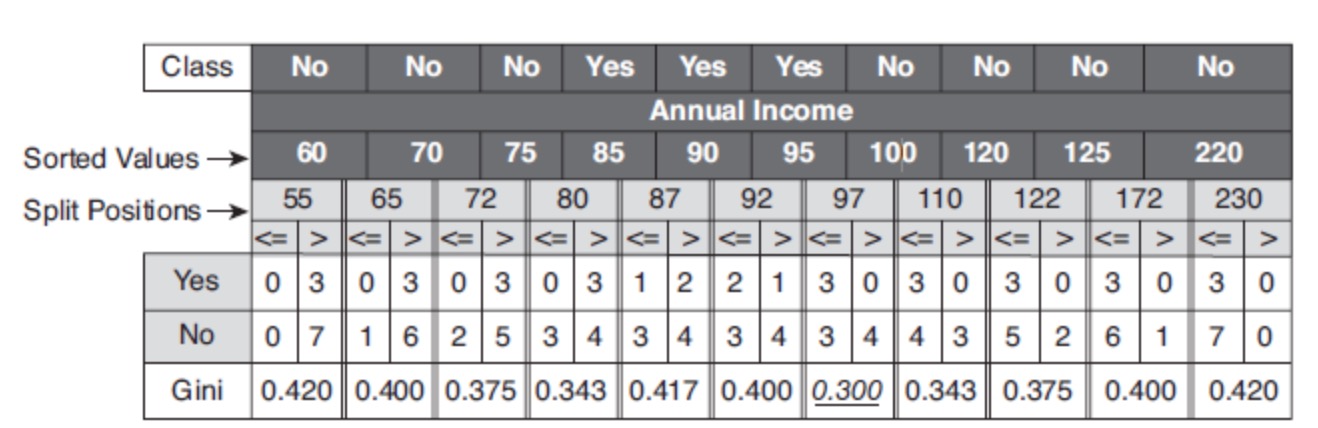
接下来，需要解决的问题：应该选择哪种特征属性及定义条件，才能分类效果比较好。CART 采用 Gini指数 来度量分裂时的不纯度，之所以采用Gini指数，是因为较于熵而言其计算速度更快一些。对决策树的节点 t，Gini指数计算公式如下：
\[ Gini(t) = 1 - \sum_{k} {p(c_k|t)^2} \]
Gini指数 即为1与类别$ c_k $的概率平方之和的差值，反映了样本集合的不确定性程度。Gini指数 越大，样本集合的不确定性程度越高。分类学习过程的本质是样本不确定性程度的减少（即熵减过程），故应选择最小 Gini指数 的特征分裂。父节点对应的样本集合为 D，CART 选择特征 A 分裂为两个子节点，对应集合为 $D_L$ 与 $D_R$ ；分裂后的 Gini指数 定义如下：
\[
Gini(D,A) = \frac{\lvert{D_L}\rvert}{\lvert{D}\rvert}Gini(D_L) + \frac{\lvert{D_R}\rvert}{\lvert{D}\rvert}Gini(D_R)
\]
其中，|⋅|表示样本集合的记录数量。如上图中的表格所示，当Annual Income 的分裂值取 87 时，则 Gini指数 计算如下：
\[
Gini(D,A) = \frac{4}{10}[1 - (\frac{1}{4})^2 - (\frac{3}{4})^2] + \frac{6}{10}[1 - (\frac{2}{6})^2 - (\frac{4}{6})^2] = 0.417
\]
CART 算法过程如下：
CART 算法流程与 C4.5 算法相类似：
1.若满足停止分裂条件（样本个数小于预定阈值，或Gini指数小于预定阈值（样本基本属于同一类，或没有特征可供分裂），则停止分裂； 2.否则，选择最小Gini指数进行分裂； 3.递归执行1-2步骤，直至停止分裂。
CART 剪枝与 C4.5 的剪枝策略相似，均以极小化整体损失函数实现。同理，定义决策树 T 的损失函数为：
\[ L_α(T) = C(T) + α|T| \]
其中，C(T) 表示决策树的训练误差，α 为调节参数，|T| 为模型的复杂度。
CART算法采用递归的方法进行剪枝，具体办法：
将α递增 $ 0 = α_0<α_<α_2<…<α_n $，计算得到对应于区间 $[α_i,α_i+1)$ 的最优子树为 $T_i$；
从最优子树序列 ${T_1,T_2,⋯,T_n}$ 选出最优的（即损失函数最小的）。
如何计算最优子树为 $T_i$ 呢？首先，定义以 t 为单节点的损失函数为
\[ L_α(t) = C(t) + α \]
以 T 为根节点的子树 T_t 的损失函数为
\[ L_α(t) = C(t) + α \]
为单节点的损失函数为
\[ L_α(T_t) = C(T_t) + α|T_t| \]
令$ L_α(t) = L_α(T_t) $
则得到：
\[ α = \frac{C(t) - C(T_α)}{|T_α| - 1} \]
此时，单节点t与子树$T_t$有相同的损失函数，而单节点t的模型复杂度更小，故更为可取；同时也说明对节点 t 的剪枝为有效剪枝。由此，定义对节点t的剪枝后整体损失函数减少程度为：
\[
g(t) = \frac{C(t) - C(T_t)}{|T_t| - 1}
\]
剪枝流程如下：
g(t)；选择最小的 g(t) 作为 α1 ，并进行剪枝得到树 $T_1$，其为区间 $[α_1,α_2)$ 对应的最优子树。g(t)… $α_2$…$T_2$…笔记是英文的，单词句子很简单就不做翻译了 。
CART - Classificcation And Regression Tree
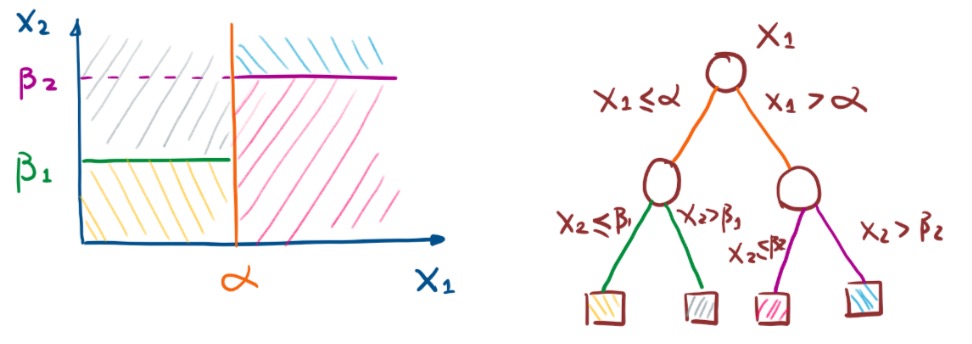
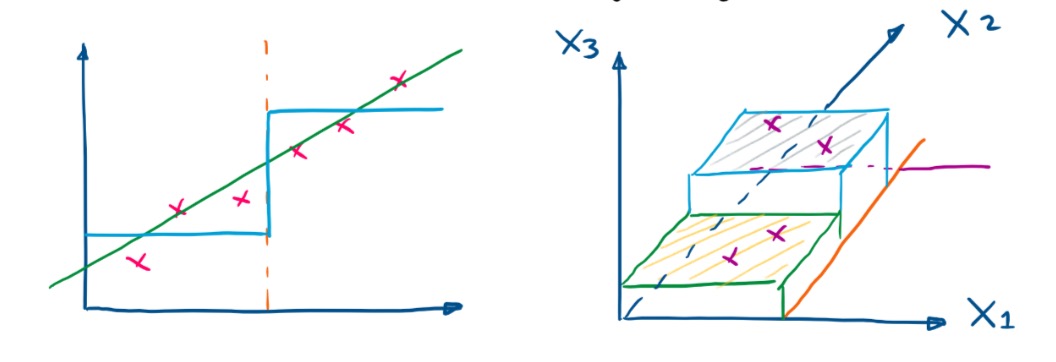
We find the best variable $x_j$ and cut points inorder to minize the loss function.\[
Loss = \min_{j,s} {[ \min_{C_1}{\sum_{x ∈R_1(j,s)} {(y^{(i)} - C_1)^2}} + \min_{C_2}{\sum_{x ∈R_2(j,s)} {(y^{(i)} - C_2)^2}} ]}
\]
where\[ C_m = \frac{1}{N_m} \sum_{x ∈ R_m(j,s)}{y^{(i)}} , m = 1,2\]
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
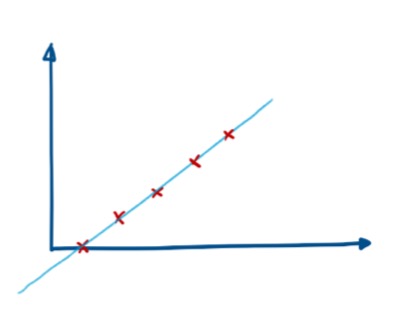(j = 1)
Given s = 1.5
$ R_1 = { 0 } $, $ C_1 = 0 $
$ R_2 = { 1, 2, …, 9 } $, $ C_2 = 5 $
\[ Loss(1.5) = 0^2 + \sum_{i = 1}^{9} {(i - 5)^2} \]
Given s = 4.5 $ R_1 = { 0, 1, 2, 3 } $, $ C_1 = 1.5 $ $ R_2 = { 4, 5, 6, 7, 8, 9 } $, $ C_2 = 6.5 $ \[ Loss(4.5) =\sum_{i = 0}^{3} {(i - 5)^2} + \sum_{i = 4}^{9} {(i - 6.5)^2} \] calculate Loss(s) for s = 1.5, 2.5, …, 9.5 find the best cut point s.
if no more than on variable, search (j = 1, …, n) with best cut point $s_j$
Bootstrapping 从字面意思翻译是 拔靴法，从其内容翻译又叫自助法，是一种再抽样的统计方法。自助法的名称来源于英文短语 “to pull oneself up by one’s bootstrap”，表示完成一件不能自然完成的事情。1977年美国Standford大学统计学教授Efron提出了一种新的增广样本的统计方法，就是Bootstrap方法，为解决小子样试验评估问题提供了很好的思路。
算法流程
N 个样本中有放回的随机抽取 n 个样本。n 个样本计算统计量m 次，得到统计量bootstrapping 方法就是通过多次的随机采样得到可以代表母体样本分布的子样本分布）应该说是Bootstrap是现代统计学较为流行的方法，小样本效果好，通过方差的估计可以构造置信区间等。
Bagging即套袋法，可译为自主整合法，Booststrapping is any test or metric that relies on random sampling with replacement（放回式采样）。其算法过程如下：
N个样本中有放回的随机抽取 n 个样本。n 个样本的所有属性构建基分类器（LR,ID3,C4.5,SVM）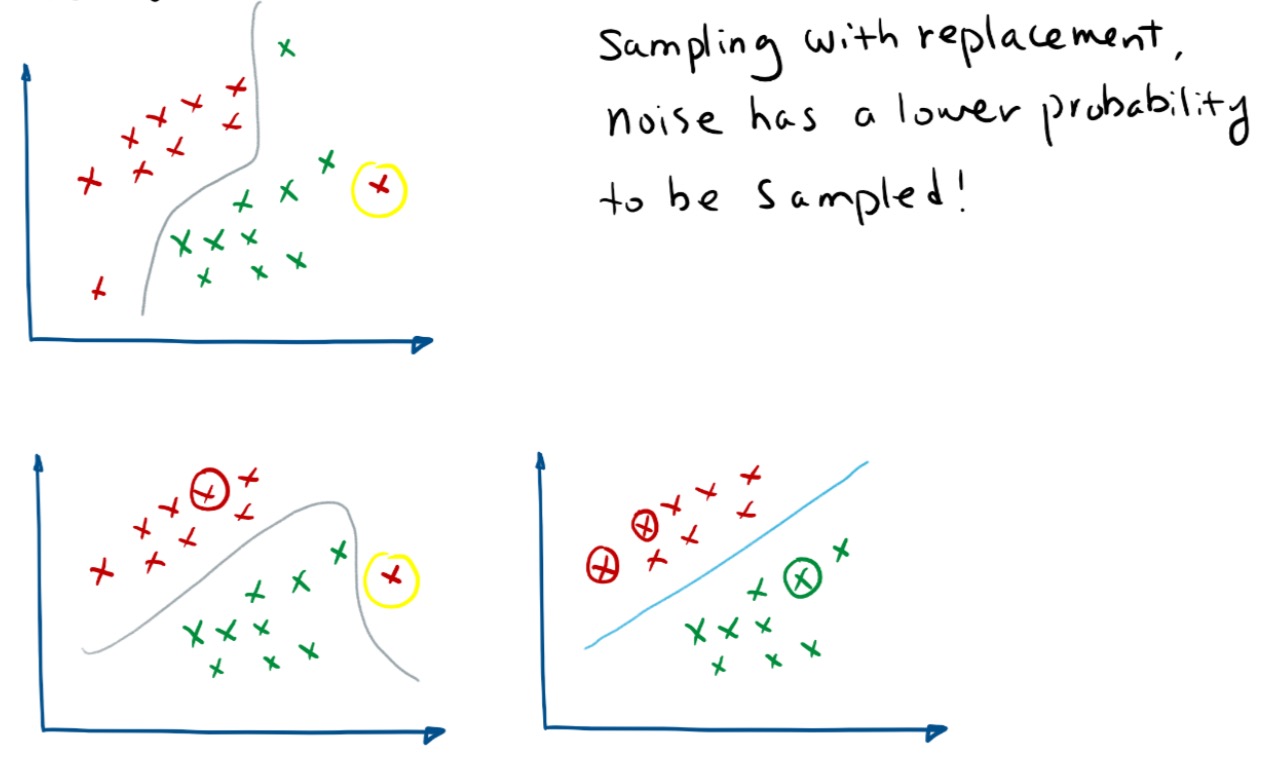
其主要思想是将弱分类器组装成强分类器。在PAC(概率近似正确)的框架下，则一定可以将一个弱分类器组装成一个强分类器。
关于 Boosting 的两个核心问题：
1. 在每一轮如何改变训练数据的权值或概率分布？
通过提高前一轮中被弱分类器分错样例的权值，减少前一轮对样例的权值，来使分类区对误分的数据有较好的效果。
2. 通过什么方式在组合弱分类器？
通过加法模型将弱分类器线性组合，比如Aadaboost 通过加权多次表决的方式，即增大错误率小的分类器的权值，同时减小错误率大的分类器的权值。而提升树通过拟合残差的方式逐步减小误差，将每一步生成模型叠加得到最终模型。
Bagging和Boosting都是将已有的分类或回归算法通过一定方式组合起来，形成一个性能更加强大的分类器，更准确的说这是一种分类算法的组装方法。即将弱分类器组装成强分类器的方法。
样本选择上 Bagging: 训练集在样本集中有放回选取，从原实际中选出的各轮训练集之间是独立的。 Boosting: 每一轮的训练集不变，只是训练集中每一个样例在分类器中的权重发生变化。而权重是根据上一轮的分类结果进行调整的。
样例权重 Bagging: 使用均匀取样，每个样例权重相等。 Boosting: 根据错误率不断调整样本的权值，错误率却大则权重越大。
预测函数 Bagging: 使所有预测函数的权重相等。 Boosting: 每个弱分类器都有相应的权重，对于分类误差小的分类器，会有更大的权重。
并行计算 Bagging: 各个误差函数可以并行生成。 Boosting: 每个误差函数只能顺序生成，因为后一个模型参数需要前一轮模型结果。
这两种方法都是把若干个分类器整合为一个分类器的方法，只是整合的方式不一样，最终得到不一样的效果，将不同的分类算法套入到此类算法框架中一定程度上会提高了原单一分类器的分类效果，但是也增大了计算量。
下面是将决策树与这些算法框架进行结合所得到的新的算法：
1）Bagging + 决策树 = 随机森林
2）AdaBoost + 决策树 = 提升树
3）Gradient Boosting + 决策树 = GBDT
boosting 是一种思想，Gradient Boosting 是一种实现 Boosting 的方法，它的主要思想是，每一次建立模型，是在之前建立模型损失函数的梯度下降方向。损失函数描述的是模型的不靠谱程度，损失函数越大，说明模型越容易出错。如果我们的模型能够让损失函数持续的下降，说明我们的模型在不停的改进，而最好的方式就是让损失函数在其梯度的方向下降。
为什么说bagging是减少variance，而boosting是减少bias？