Decision Tree algorithm（四）

目录：

• Decision Tree algorithm（四）
  • 一. Tree Ensembles - Random Forest
    • 随机森林 (Bagging with CARTs)
      • 定义
      • 算法
      • 优缺点
  • 二. Tree Ensembles - Gradient Boosting Decision Tree(GBDT)
  • 三. 参考文献

一. Tree Ensembles - Random Forest

随机森林 (Bagging with CARTs)

定义

bagging方法可以有效降低模型的方差。随机森林每棵子树不需要剪枝，是低偏差高方差的模型，通过bagging降低方差后使得整个模型有较高的性能。

算法

随机森林算法如下:

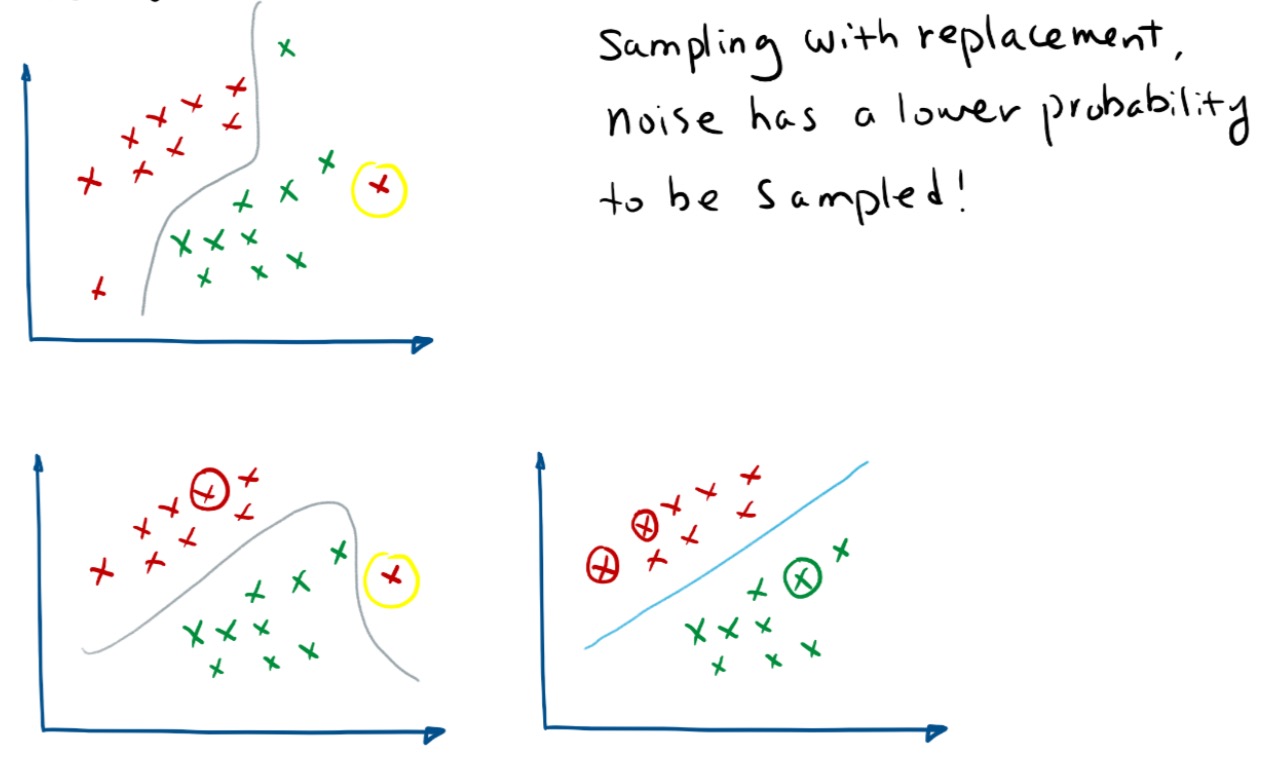
1. 从N个样本中有放回的随机抽样n个样本。

2. 如果每个样本的特征维度为 M，指定一个常数 m«M，随机地从M个特征中选取m个特征子集，每次树（ID3,C4.5,CART）进行分裂时，从这m个特征中选择最优的(信息增益，信息增益比率，基尼系数)；

3. 每棵树都尽最大程度的生长，并且没有剪枝过程。

4. 采用投票表决的方式进行分类。

特征m个数的选取： 用作分类时，m默认取，最小取1. 用作回归时，m默认取M/3，最小取5.

两个随机性的引入对随机森林的分类性能至关重要。由于它们的引入，使得随机森林不容易陷入过拟合，并且具有很好得抗噪能力（比如：对缺省值不敏感）。

随机森林分类效果（错误率）与两个因素有关： 森林中任意两棵树的 相关性：相关性越大，错误率越大； 森林中每棵树的 分类能力：每棵树的分类能力越强，整个森林的错误率越低。

减小特征选择个数m，树的相关性和分类能力也会相应的降低；增大m，两者也会随之增大。所以关键问题是如何选择最优的m（或者是范围），这也是随机森林唯一的一个参数。 　　 　　

优缺点

随机森林优点：

1. 具有极高的准确率
2. 随机性的引入，使得随机森林不容易过拟合
3. 随机性的引入，使得随机森林有很好的抗噪声能力
4. 能处理很高维度的数据，并且不用做特征选择
5. 既能处理离散型数据，也能处理连续型数据，数据集无需规范化
6. 训练速度快，可以得到变量重要性排序
7. 容易实现并行化

随机森林缺点：

1. 当随机森林中的决策树个数很多时，训练时需要的空间和时间会较大
2. 随机森林模型还有许多不好解释的地方，有点算个黑盒模型

二. Tree Ensembles - Gradient Boosting Decision Tree(GBDT)

三. 参考文献

[1] 李航，《统计学习方法》

[2] 陈云樱等, 《决策树中基于基尼指数的属性分裂方法》