目录:
决策树(decision tree)算法基于特征属性进行分类,其主要的优点:模型具有可读性,计算量小,分类速度快。决策树算法包括了由Quinlan提出的ID3与C4.5,Breiman等提出的CART。其中,C4.5是基于ID3的,对分裂属性的目标函数做出了改进。
决策树是一种通过对特征属性的分类对样本进行分类的树形结构,包括有向边与三类节点:
根节点(root node):表示第一个特征属性,只有出边没有入边;
内部节点(internal node):表示特征属性,有一条入边至少两条出边;
叶子节点(leaf node):表示类别,只有一条入边没有出边。
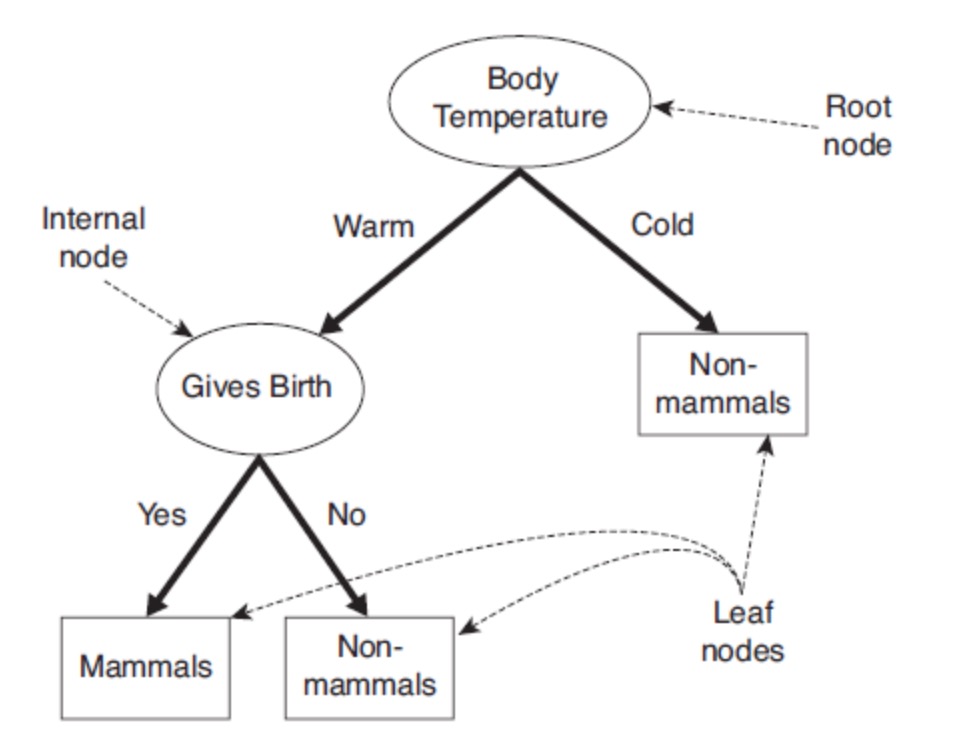
上图给出了(二叉)决策树的示例。决策树具有以下特点:
对于二叉决策树而言,可以看作是if-then规则集合,由决策树的根节点到叶子节点对应于一条分类规则;
分类规则是互斥并且完备的,所谓互斥即每一条样本记录不会同时匹配上两条分类规则,所谓完备即每条样本记录都在决策树中都能匹配上一条规则。
分类的本质是对特征空间的划分,如下图所示,
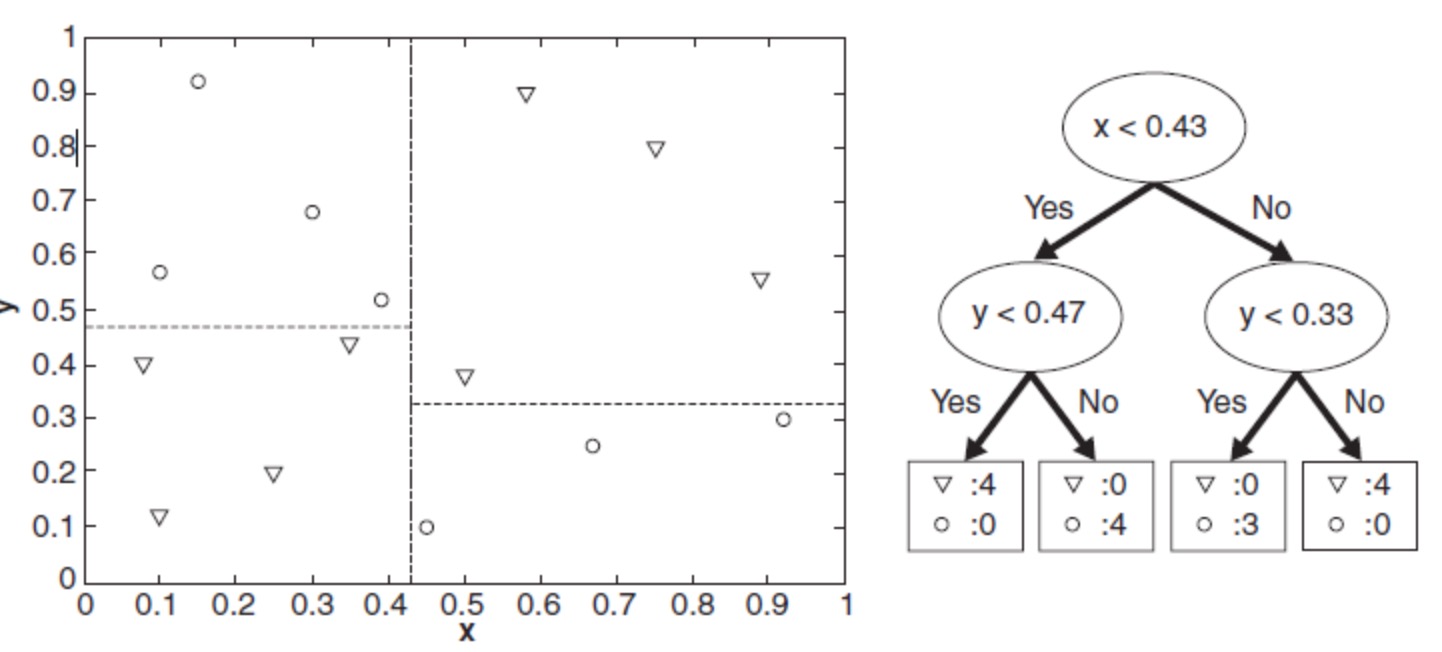
决策树学习的本质是从训练数据集中归纳出一组分类规则。但随着分裂属性次序的不同,所得到的决策树也会不同。如何得到一棵决策树既对训练数据有较好的拟合,又对未知数据有很好的预测呢?
首先,我们要解决两个问题:
如何选择较优的特征属性进行分裂?每一次特征属性的分裂,相当于对训练数据集进行再划分,对应于一次决策树的生长。ID3算法定义了目标函数来进行特征选择。
什么时候应该停止分裂?有两种自然情况应该停止分裂,一是该节点对应的所有样本记录均属于同一类别,二是该节点对应的所有样本的特征属性值均相等。但除此之外,是不是还应该其他情况停止分裂呢?
在信息论中,自信息(英语:self-information),由克劳德·香农提出,是与概率空间中的单一事件或离散随机变量的值相关的信息量的量度。它用信息的单位表示,例如 bit、nat或是hart,使用哪个单位取决于在计算中使用的对数的底。自信息的期望值就是信息论中的熵,它反映了随机变量采样时的平均不确定程度。
由定义,当信息被拥有它的实体传递给接收它的实体时,仅当接收实体不知道信息的先验知识时信息才得到传递。如果接收实体事先知道了消息的内容,这条消息所传递的信息量就是0。只有当接收实体对消息对先验知识少于100%时,消息才真正传递信息。
因此,一个随机产生的事 $ω_n$ 所包含的自信息数量,只与事件发生的机率相关。事件发生的机率越低,在事件真的发生时,接收到的信息中,包含的自信息越大。$ω_n$ 的自信息量:
\[ I(ω_n) = f(P(ω_n)) \]
如果$ P(ω_n) = 1$,则 $I(ω_n) = 0$。如果$ P(ω_n) < 1$, 则 $I(ω_n) > 0$。此外,根据定义,自信息的量度是非负的而且是可加的。如果事件 C 是两个独立事件 A 和 B 的交集,那么宣告 C 发生的信息量就等于分别宣告事件 A 和事件 B 的信息量的和:
\[ I(C) = I(A∩B) = I(A) + I(B) \]
因为 A 和 B 是独立事件,所以 C 的概率为:
\[ P(C) = P(A∩B) = P(A) · P(B) \]
应用函数 f(·) 会得到:
\[ I(C) = I(A) + I(B) \]
\[ f(P(C)) = f(P(A)) + f(P(B)) = f(P(A) · P(B)) \]
所以函数 f(·) 具有性质
\[ f(x·y) = f(x) + f(y) \]
而对数函数正好有这个性质,不同的底的对数函数之间的区别只差一个常数:
\[ f(x) = Klog(x) \]
由于事件的概率总在 0 和 1 之间,而信息量不能为负,所以 K<0 。考虑到这些性质,假设事件 $ω_n$ 发生的机率是 $P(ω_n)$ ,自信息量的 $I(ω_n)$ 的定义为:
\[ I(ω_n) = -log(P(ω_n)) = log(\frac{1}{P(ω_n)}) \]
事件 $ω_n$ 的概率越小, 它发生后的自信息量越大。此定义符合上述条件。在上面的定义中,没有指定的对数的基底:如果以 2 为底,单位是 bit。当使用以 e 为底的对数时,单位将是 nat。对于基底为 10 的对数,单位是 hart。信息量的大小不同于信息作用的大小,这不是同一概念。信息量只表明不确定性的减少程度,至于对接收者来说,所获得的信息可能事关重大,也可能无足轻重,这是信息作用的大小。
和熵的联系 熵是离散随机变量的自信息的期望值。但有时候熵也会被称作是随机变量的自信息,可能是因为熵满足 $H(X) = I(X;X)$,而 $I(X;X)$ 是 X 和它自己的互信息。
在概率论和信息论中,两个随机变量的 互信息(Mutual Information,简称MI) 或 转移信息(transinformation) 是变量间相互依赖性的量度。不同于相关系数,互信息并不局限于实值随机变量,它更加一般且决定着联合分布 p(X,Y) 和分解的边缘分布的乘积 p(X)p(Y) 的相似程度。互信息是 点间互信息(PMI) 的期望值。互信息最常用的单位是 bit。
一般地,两个离散随机变量 X 和 Y 的互信息可以定义为:
\[
I(X;Y) = \sum_{y∈Y}\sum_{x∈X}{P(x,y)log(\frac{P(x,y)}{P(x)·P(y)})} \]
其中 p(x,y) 是 X 和 Y 的联合概率分布函数,而 P(x) 和 P(y) 分别是 X 和 Y 的边缘概率分布函数。
在连续随机变量的情形下,求和被替换成了二重定积分:
\[ I(X;Y) = \int_{Y}\int_{X}{P(x,y)log(\frac{P(x,y)}{P(x)·P(y)})} {\rm d}x{\rm d}y \]
其中 P(x,y) 当前是 X 和 Y 的联合概率密度函数,而 P(x) 和 P(y) 分别是 X 和 Y 的边缘概率密度函数。如果对数以 2 为基底,互信息的单位是 bit。
直观上,互信息度量 X 和 Y 共享的信息:它度量知道这两个变量其中一个,对另一个不确定度减少的程度。例如,如果 X 和 Y 相互独立,则知道 X 不对 Y 提供任何信息,反之亦然,所以它们的互信息为零。在另一个极端,如果 X 是 Y 的一个确定性函数,且 Y 也是 X 的一个确定性函数,那么传递的所有信息被 X 和 Y 共享:知道 X 决定 Y 的值,反之亦然。因此,在此情形互信息与 Y(或 X)单独包含的不确定度相同,称作 Y(或 X)的熵。而且,这个互信息与 X 的熵和 Y 的熵相同。(这种情形的一个非常特殊的情况是当 X 和 Y 为相同随机变量时。)
互信息是 X 和 Y 的联合分布相对于假定 X 和 Y 独立情况下的联合分布之间的内在依赖性。 于是互信息以下面方式度量依赖性:I(X; Y) = 0 当且仅当 X 和 Y 为独立随机变量。从一个方向很容易看出:当 X 和 Y 独立时,p(x,y) = p(x) p(y),因此,
\[ log(\frac{P(A,B)}{P(A)·P(B)}) = log(1) = 0 \]
此外,互信息是非负的(即 I(X;Y) ≥ 0),而且是对称的(即 I(X;Y) = I(Y;X))。
另外,互信息可以简单的表示成:
\[ I(X;Y) = H(Y) - H(Y|X) = H(X,Y) - H(X|Y) - H(Y|X) \]
其中 H(X) 和 H(Y) 是边缘熵,H(X|Y) 和 H(Y|X) 是条件熵,而 H(X,Y) 是 X 和 Y 的联合熵。直观地说,如果把熵 H(Y) 看作一个随机变量于不确定度的量度,那么 H(Y|X) 就是”在已知 X 事件后Y事件会发生”的不确定度。这证实了互信息的直观意义为: “因X而有Y事件”的熵(基于已知随机变量的不确定性) 在”Y事件”的熵之中具有多少影响地位(“Y事件所具有的不确定性” 其中包含了多少 “Y|X事件所具有的不确性” ),意即”Y具有的不确定性”有多少程度是起因于X事件。
舉例來說,當
I(X;Y) = 0時,也就是H(Y) = H(Y|X)時,即代表此時"Y的不確定性"即為"Y|X的不確定性",這說明了互信息的具體意義是在度量兩個事件彼此之間的關聯性。
所以具体的解释就是:互信息越小,两个来自不同事件空间的随机变量彼此之间的关联性越低;互信息越高,关联性则越高。
在信息论中,熵(英语:entropy)是接收的每条消息中包含的信息的平均量,又被称为信息熵、信源熵、平均自信息量。这里,“消息”代表来自分布或数据流中的事件、样本或特征。(熵最好理解为不确定性的量度而不是确定性的量度,因为越随机的信源的熵越大。)
\[ H(X) = E[I(X)] = E[-ln[P(X)]] \]
其中,P 为 X 的概率质量函数(probability mass function),E 为期望函数,而 I(X) 是 X 的信息量(又称为自信息)。I(X) 本身是个随机变数。当取自有限的样本时,熵的公式可以表示为:
\[
H(X) = \sum_{i} {P(x_i)I(x_i)} = -\sum_{i} {P(x_i)log_b{P(x_i)}}
\]
可以定义事件 X 与 Y 分别取 x_i 和 y_j 时的条件熵为:
\[ {H(X|Y)} = -\sum_{i,j}{P(x_i,y_j)·log[\frac{P(x_i,y_j)}{P(y_j)}]} \]
这个量应当理解为你知道Y的值前提下随机变量 X 的随机性的量。
相对熵(relative entropy)又称为KL散度(Kullback–Leibler divergence,简称KLD),信息散度(information divergence),信息增益(information gain)。
KL散度是两个概率分布 P 和 Q 差别的非对称性的度量。 KL散度是用来度量使用基于 Q 的编码来编码来自 P 的样本平均所需的额外的位元数。典型情况下,P 表示数据的真实分布,Q 表示数据的理论分布,模型分布,或 P 的近似分布。 对于离散随机变量,其概率分布 P 和 Q 的KL散度可按下式定义为
\[ D_KL(P||Q) = -\sum_{i}{P(i)\frac{Q(i)}{P(i)}} \]
等价于
\[ D_KL(P||Q) = \sum_{i}{P(i)\frac{P(i)}{Q(i)}} \]
即按概率 P 求得的 P 和 Q 的对数差的平均值。KL散度仅当概率 P 和 Q 各自总和均为 1,且对于任何 i 皆满足Q(i)>0及P(i)>0时,才有定义。式中出现 0ln0 的情况,其值按0处理。
对于连续随机变量,其概率分布 P 和 Q 可按积分方式定义为:
\[ D_KL(P||Q) = \int_{-∞}^{∞}{P(i)\frac{Q(i)}{P(i)}}{\rm d}x \]
尽管从直觉上KL散度是个度量或距离函数, 但是它实际上并不是一个真正的度量或距离。因为KL散度不具有对称性:从分布 P 到 Q 的距离通常并不等于从 Q 到 P 的距离。
举个栗子:
对于一维数据来说:\[ 对总体的信息熵: ori-Entropy(x) = -\frac{1}{2}log\frac{1}{2} - \frac{1}{2}log\frac{1}{2} = 1 \] 对于
A点来说,左边的信息熵用A_1表示,右边用A_2表示,则有 \[ Entropy(A_1) = 0, Entropy(A_2) = -\frac{2}{7}log\frac{2}{7} - \frac{5}{7}log\frac{5}{7} \] 对于信息增益(Information Gain,由于熵的减小,增加信息量的多少): \[ IG = ori-Entropy - \sum_{i=1}^n{ω_i}{Entropy(A_i)} \] 即: \[ IG = Entropy(A) - \sum_{i=1}^n{\frac{\lvert{A_i}\rvert}{A}}{Entropy(A_i)} \] 所以有A点处的信息增益为: \[ IG(A) = 1 - \frac{3}{10}×0 + \frac{7}{10}×Entropy(A_2) \] 所以,B点处的信息增益为: \[ IG(B) = 1 - \frac{6}{10}×Entropy(B_1) + \frac{4}{10}×Entropy(B_2) \] 同理可求出IG(C),选择IG(A),IG(B),IG(C)中的最大值就是划分的最佳结点。
再比如上回提到的 Play Tennis 的预测模型:以上的步骤就是
ID3算法(根据信息增益,确定合适的节点)的基本思路,实际就是将空间分为很多区域,根据特征类型进行划分,我们可以将空间划分为:ordinal(有序的),numerial(数字的),discrete(离散的)。对于子树(sub-Trees)的选择,取决于两个属性:attribute types(Nominal, Ordinal, Continuous),number of ways to split(2-way split, Muti-way split)。对于连续数据的离散化(Discretization)可以根据数据分布,区域,熵进行离散化。对于分割(splitting),有Muti-way split(Use as many partitions as distinct values.) 和Binary split(Divide values into two subject. Need to find optional partitioning.) 两种。
以信息增益比作为划分训练数据集的特征,存在偏向于选择取值较多的特征的问题。使用信息增益比(Information gain ratio)可以对这一问题进行校正,这是特征选择的标准之一。
特征 A 对数据集 D 的信息增益比g_r(D,A)定义为信息增益g(D,A)与训练数据集 D 关于特征 A 的值的熵H_A(D)之比,即
\[ g_R(D,A) = \frac{g(D,A)}{H_A(D)} \]
其中,
\[ -\sum_{i=1}^n{\frac{\lvert{D_i}\rvert}{\lvert{D}\rvert}{log}_2}{\frac{\lvert{D_i}\rvert}{\lvert{D}\rvert}} \]
n 是特征 A 取值的个数。
对于给定样本集合 D,其 GINI Index(基尼系数)为:
\[ GINI(D) = 1 - \sum_{k=1}^K{[\frac{\lvert{C_k}\rvert}{\lvert{D}\rvert}]}^2 \]
其中 $C_k$ 是 D 中属于第 k 类的样本子集, K 是类的个数。
举个栗子: 如果中有 $C_1$ 类
0个,$C_2$ 类6个,则GINI系数为: \[ GINI(C) = 1 - \sum_{i=1}^2{[\frac{\lvert{C_i}\rvert}{\lvert{D}\rvert}]}^2 = 1 - [[\frac{0}{6}]^2 + [\frac{6}{6}]^2] = 0 \] 如果中有 $C_1$ 类3个,$C_2$ 类3个,则GINI系数为: \[ GINI(C) = 1 - \sum_{i=1}^2{[\frac{\lvert{C_i}\rvert}{\lvert{D}\rvert}]}^2 = 1 - [[\frac{3}{6}]^2 + [\frac{3}{6}]^2] = \frac{1}{2} \]
基尼系数具有以下特点:
GINI Split:
Used in CART, SLIQ, SPRINT.
When a node p is split into k partitions (children), the quality of split is computed as,
\[
GINI_(split) = 1 - \sum_{i=1}^{k} {\frac{n_i}{n}GINI(i)}
\]
where, n_i = number of records at child i, n = number of records at node p.
For efficient computation:
for each attribute,
For an example:
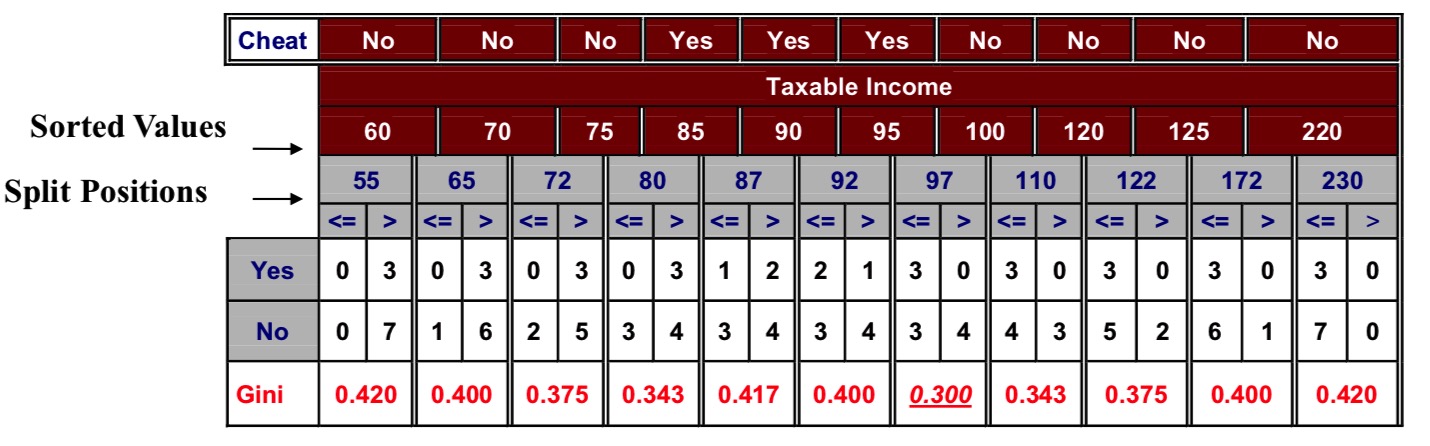
基尼指数的基本思想是:对每个属性都遍历所有的分割方法后若能提供最小的 GINI_Split,就被选择作为此节点处分裂的标准,无论处于根节点还是子节点。
\[ Error(t) = 1 - max P(i|t) \]
举个栗子:
 Measure of Impurity for 2-Class Problems:
Measure of Impurity for 2-Class Problems: