From Word Embeddings To Document Distances 论文总结

目录：

• From Word Embeddings To Document Distances 论文总结
  • 几种词向量表示方法
    • One-Hot Encoding
    • BOW（Bag-Of-Word）
    • TF-IDF
    • word2vec
  • From Word Embeddings To Document Distances
    • EMD
    • WMD
    • 优化
  • 参考文献

文章提出了一种基于Word2Vec来衡量文档间相似性的方法，称之为词移距离，并提出两种优化方法。首先，衡量两篇文章的相似性，我们将文章中的每个词映射在词向量空间。我们为每一个词设置一个权重，文档1中的每一个词和文档2中的每一个词都进行匹配，而且文档1中的每一个词的权重等于这个词对应到文档2中每个词的权重之和，同样的道理，文档2中每个词的权重等于这个词接收到的来自文档1的所有词的权重之和。另外，我们将每个词对之间的距离作为代价。这样计算出的总代价称为最终两个文档的相似程度。这个问题直接可以转化为线性规划中的EMD（Earth Mover's Distance）问题的一个实例，找到最优解。作者提出两种优化算法，一种是寻找WMD问题的lower bounds，另一种是Relaxed word moving distence，将算法的复杂度从 $ O(p^3logp) $ 降为 $O(p^2)$，p表示文档1中有而文档2中没有的单词个数。

几种词向量表示方法

One-Hot Encoding

One-Hot编码，又称为一位有效编码，主要是采用位状态寄存器来对个状态进行编码，每个状态都由他独立的寄存器位，并且在任意时候只有一位有效。在实际的机器学习的应用任务中，特征并不总是连续值，有可能是一些离散值值，如性别可分为“male”和“female”。在回归，分类，聚类等机器学习算法中，特征之间距离的计算或相似度的计算是非常重要的，而我们常用的距离或相似度的计算都是在欧式空间的相似度计算，计算余弦相似性，基于的就是欧式空间。而我们使用One-Hott编码，将离散特征的取值扩展到了欧式空间，离散特征的某个取值就对应欧式空间的某个点。将离散型特征使用One-Hot编码，确实会让特征之间的距离计算更加合理。One-Hot编码就是将出现过的特征的所有可能性使用二进制编码的方式表示出来，需要时使用二进制的编码的方式表示。举个栗子，以下为一个特征列表，我们需要一个（大妈，30，北海）的特征，应该怎么表示呢？

name	age	region
路飞	18	北海
明哥	30	新世界
凯多	40	新世界
大妈	50	新世界

One-Hot Encoding 将每个特征的所有可能性表示为一个特征列表，name表示为（路飞，明哥，凯多，大妈），age表示为（18，30，40，50），region表示为（北海，新世界）。要表示的特征在特征列表中出现则为 1，不出现则为 0。大妈这个特征表示为0001, 30 表示为 0101,北海表示为10。这样不管出现什么要表示的特征，都可以在特征列表中找到，并以二进制的形式表示出来。最终特征（大妈，30，北海）用One-Hot Encoding表示为0001 0101 10。

用这种表示方法的缺点在于：

1. 如果文本中单词过多，那么出现矩阵稀疏。
2. 虽然可以计算距离，但是无法表示单词语义级别的联系。
3. 未考虑到词序，因为单词的出现词序对语义的理解也是至关重要的。

BOW（Bag-Of-Word）

Bag-of-words 模型又称为词袋模型，是信息检索领域常用的文档表示方法。在信息检索中，BOW模型假定对于一个文档，忽略它的单词顺序和语法、句法等要素，将其仅仅看作是若干个词汇的集合，文档中每个单词的出现都是独立的，不依赖于其它单词是否出现。也就是说，文档中任意一个位置出现的任何单词，都不受该文档语意影响而独立选择的。举个栗子，有如下两个文档：

1. 路飞打败了多弗朗明哥。
2. 路飞还没有打败大妈。

基于这两个文本文档，构造一个词典：{路飞,打败,了,多弗朗明哥,还,没有,大妈},那么可以将上边两句话向量化表示为：

1. [1，1，1，1，0，0，0]
2. [1，1，0，0，1，1，1]

这种方法对文档单词进行建模的缺点也很明显：

1. 也会出现矩阵稀疏。
2. 无法表示单词语义级别的联系。
3. 未考虑到词序。

TF-IDF

TF-IDF（Term Frequency–Inverse Document Frequency）是一种用于信息检索与文本挖掘的常用加权技术。TF-IDF 是一种统计方法，用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中出现的频率成反比下降。简单的解释为，一个单词在一个文档中出现次数很多，同时在其他文档中出现此时较少，那么我们认为这个单词对该文档是非常重要的。

在一份给定的文件里，词频（term frequency，tf）指的是某一个给定的词语在该文件中出现的频率。这个数字是对词数（term count）的归一化，以防止它偏向长的文件。（同一个词语在长文件里可能会比短文件有更高的词数，而不管该词语重要与否。）对于在某一特定文件里的词语 $t_i$ 来说，它的重要性可表示为： \[ tf_{i,j} = \frac{n_{i,j}}{\sum_{k}{n_{k,j}}} \] 以上式子中 $n_{i,j}$ 是该词在文件 $d_j$ 中的出现次数，而分母则是在文件 $d_j$ 中所有字词的出现次数之和。

逆向文件频率（inverse document frequency，idf） 是一个词语普遍重要性的度量。某一特定词语的idf，可以由总文件数目除以包含该词语之文件的数目，再将得到的商取以10为底的对数得到： \[ idf_i = \log{\frac{\vert{D}\vert}{| { j:t_i \in d_i }|}} \] 其中: |D|：语料库中的文件总数 $ \vert{ {j:t_i \in d_i }}\vert $：包含词语 $t_i$ 的文件数目（即 $n_{i,j} \neq 0$ 的文件数目）如果词语不在数据中，就导致分母为零，因此一般情况下使用 \[ 1 + \vert{ {j:t_i \in d_i }}\vert \] 然后通过下面公式计算tf-idf值: \[ tfidf_{i,j} = tf_{i,j} * idf_i \] 某一特定文件内的高词语频率，以及该词语在整个文件集合中的低文件频率，可以产生出高权重的tf-idf。因此，tf-idf 倾向于过滤掉常见的词语，保留重要的词语。

举个栗子： 有很多不同的数学公式可以用来计算tf-idf。这边的例子以上述的数学公式来计算。词频（tf）是一词语出现的次数除以该文件的总词语数。假如一篇文件的总词语数是100个，而词语“路飞”出现了3次，那么“路飞”一词在该文件中的词频就是3/100=0.03。而计算文件频率（IDF）的方法是以文件集的文件总数，除以出现“路飞”一词的文件数。所以，如果“路飞”一词在1,000份文件出现过，而文件总数是10,000,000份的话，其逆向文件频率就是lg（10,000,000 / 1,000）=4。最后的tf-idf的分数为0.03 * 4=0.12。

word2vec

上边叙述了两个语言模型，但均未考虑到词序的问题。使用word2vec的方法可以得到固定长度的词向量，不仅能够不捕捉到单词之间的语义和句法信息，而且能够保持词和词之间的语义关系。word2vec提出了两种语言模型，就训练得到的词向量效果而言，skip-gram模型好于CBOW。这两个模型可以看做计算word embedding的工具，word2vec中从输入到隐层的过程就是embedding的过程。Embedding的过程就是把多维的onehot进行降维的过程，是个深度学习的过程。 其好处有很多：

1. 嵌入层向量长度可设置
2. 映射过程是全连接
3. 嵌入层的值可训练
4. 由高维度映射到低纬度，减少参数量 关于这两个模型后边会使用大量篇幅来讲解，下面简单的了解一些这两个模型。

CBOW是利用上下文预测当前的单词；而Skip-Gram则是利用当前词来预测上下文。

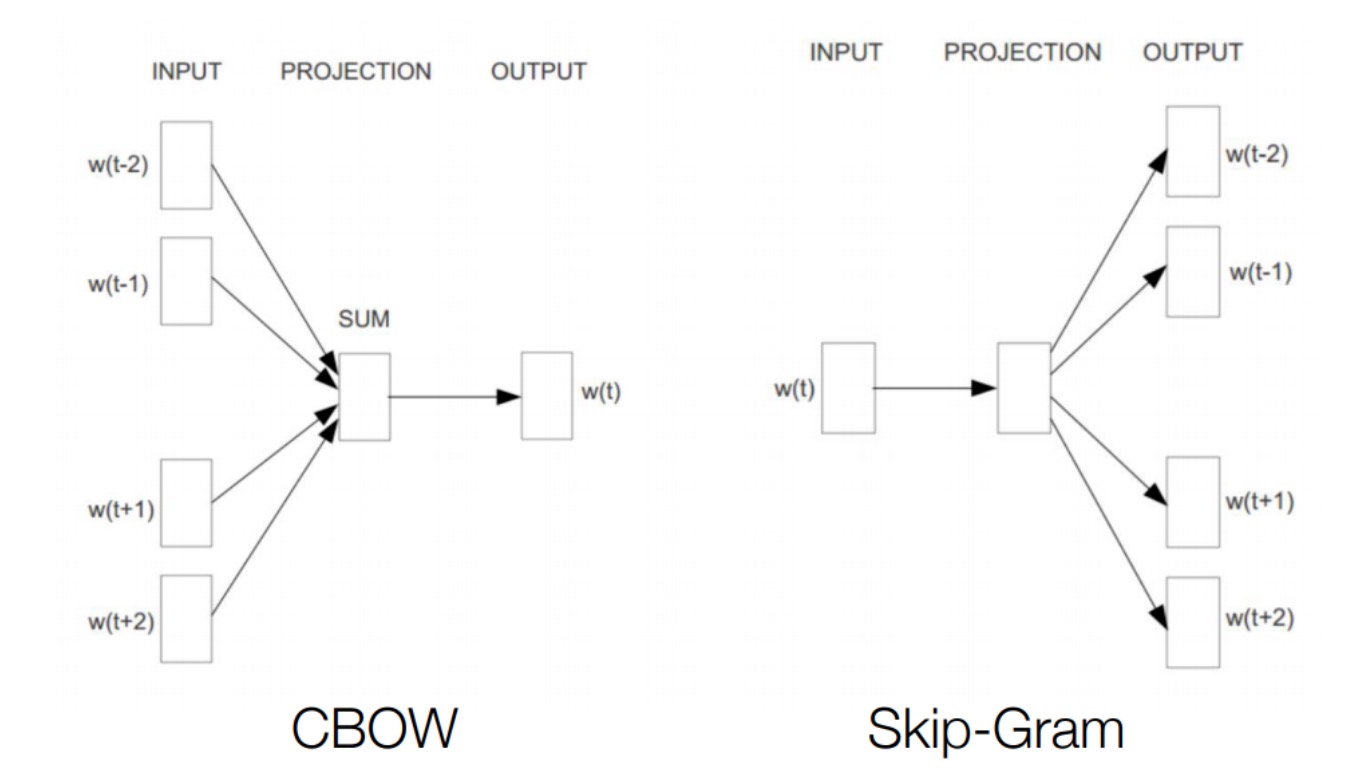
CBOW 连续词袋模型

移除前向反馈神经网络中非线性的hidden layer，直接将中间层的embedding layer与输出层的softmax layer连接；忽略上下文环境的序列信息；输入的所有词向量均汇总到同一个embedding layer；将future words纳入上下文环境。从数学上看，CBoW模型等价于一个词袋模型的向量乘以一个embedding矩阵，从而得到一个连续的embedding向量。这也是CBoW模型名称的由来。

Skip-Gram 模型

训练Skip-Gram 模型需要满足

1. 语料必须充分。一方面词典的词量要足够大，另一方面要尽可能多地包含反映词语之间关系的句子，例如，只有“鱼在水中游”这种句式在语料中尽可能地多，模型才能够学习到该句中的语义和语法关系，这和人类学习自然语言一个道理，重复的次数多了，也就会模仿了。
2. 语料必须准确。 也就是说所选取的语料能够正确反映该语言的语义和语法关系，这一点似乎不难做到，例如中文里，《人民日报》的语料比较准确。 但是，更多的时候，并不是语料的选取引发了对准确性问题的担忧，而是处理的方法。 n元模型中，因为窗口大小的限制，导致超出窗口范围的词语与当前词之间的关系不能被正确地反映到模型之中，如果单纯扩大窗口大小又会增加训练的复杂度。Skip-gram 模型的提出很好地解决了这些问题。顾名思义，Skip-gram 就是“跳过某些符号”，例如，句子“中国足球踢得真是太烂了”有4个3元词组，分别是“中国足球踢得”、“足球踢得真是”、“踢得真是太烂”、“真是太烂了”，可是我们发现，这个句子的本意就是“中国足球太烂”可是上述4个3元词组并不能反映出这个信息。Skip-gram 模型却允许某些词被跳过，因此可以组成“中国足球太烂”这个3元词组。 如果允许跳过2个词，即 2-Skip-gram。

From Word Embeddings To Document Distances

EMD

在统计学中，EMD是一个区域 D 上两个概率分布之间距离的度量。在数学中，这被称为瓦瑟斯坦度量。EMD是线性规划运输问题的最优解。让我们先简单描述下运输问题。 假设有多个工厂运输货物到多个仓库。P 从 $P_1$ 到 $P_m$ 代表 m 座工厂，工厂 $P_i$ 有重量为 $w_{P_i}$ 的货物。Q从 $Q_1$ 到 $Q_n$ 代表 n 个仓库，仓库 $Q_j$ 最大容量为 $w_{Q_j}$。如何尽可能高效地将货物从 P 运送到 Q，这就是运输问题的优化目标。 这里定义，货物从工厂 $P_i$ 到仓库 Q，距离为 $d_{ij}$，运送货物的重量为 $f_{ij}$。这样一次运输的工作量为 $d_{ij} * f_{ij}$。显然，距离越远，货物越重，工作量越大。我们需要最小化总工作量： \[ min \sum_{i=1}^m{ \sum_{j=1}^n{ d_{ij} * f_{ij} } } \] 问题有以下四个约束条件：

1. 运输过程从工厂 P 到仓库 Q，不能反向。 \[ f_{ij} \geq 0 ，1 \leq i \leq m ，1 \leq j \leq n \]
2. 从工厂$P_i$ 一次次运送出去的所有货物总量之和，不能超过该工厂所有货物的总重量$w_{P_i}$。 \[ \sum_{j=1}^n{ f_{ij} \leq w_{P_i} ，1 \leq i \leq m } \]
3. 仓库 $Q_j$ 接受的多有货物总重量不能超过仓库总容量$w_{Q_j}$。 \[ \sum_{i=1}^m{ f_{ij} \leq w_{Q_j} ，1 \leq j \leq n } \]
4. 总运输两的上限是工厂中货物总量和仓库总容量中的最小值。（这是为了避免工厂总容量和仓库总容量不一样的情况。） \[ \sum_{i=1}^m{ \sum_{j=1}^n{ f_{ij} } } = min(\sum_{i=1}^m{w_{P_i}}, \sum_{j=1}^n{w_{Q_j}}) \] 假设我们得到了最优解 $f{_{ij}}{^*}$，为了是 EMD 不会随总运输量的变化而变化，每一次的运输量还要除以总运输量，以达到归一化的目的。EMD（The earth mover's distance）定义如下：

\[ EMD(P, Q) = \frac{ \sum_{i=1}^m{ \sum_{j=1}^n{d_{ij} \ast f{{ij}}{^*}}} }{ \sum{i=1}^m{ \sum_{j=1}^n{f{_{ij}}{^*}}} } \]

WMD

Word Mover’s Distance (WMD) 中文称为 词移距离。 在word2vec中有说过，这种embedding的方法可以保留语义信息。例如：vec(Berlin) - vec(Germany) = vec(Paris) - vec(France)。这说明嵌入词向量之间的距离在某种程度上是有意义的。文章使用word2vec的方法，将文本表示为有权重的embedding word的点集。两个文本之间的距离表示为，从文档A中的每个单词的embedding点集需要和文档B中的每个单词的embedding都进行匹配，求得最小的累计距离。我们为每一个词设置一个权重，文档1中的每一个词和文档2中的每一个词都进行匹配，而且文档1中的每一个词的权重等于这个词对应到文档2中每个词的权重之和，同样的道理，文档2中每个词的权重等于这个词接收到的来自文档1的所有词的权重之和。另外，我们将每个词对之间的距离作为代价。这样计算出的总代价称为最终两个文档的相似程度。这个问题直接可以转化为线性规划中的EMD（Earth Mover's Distance）问题的一个实例，找到最优解。如图所示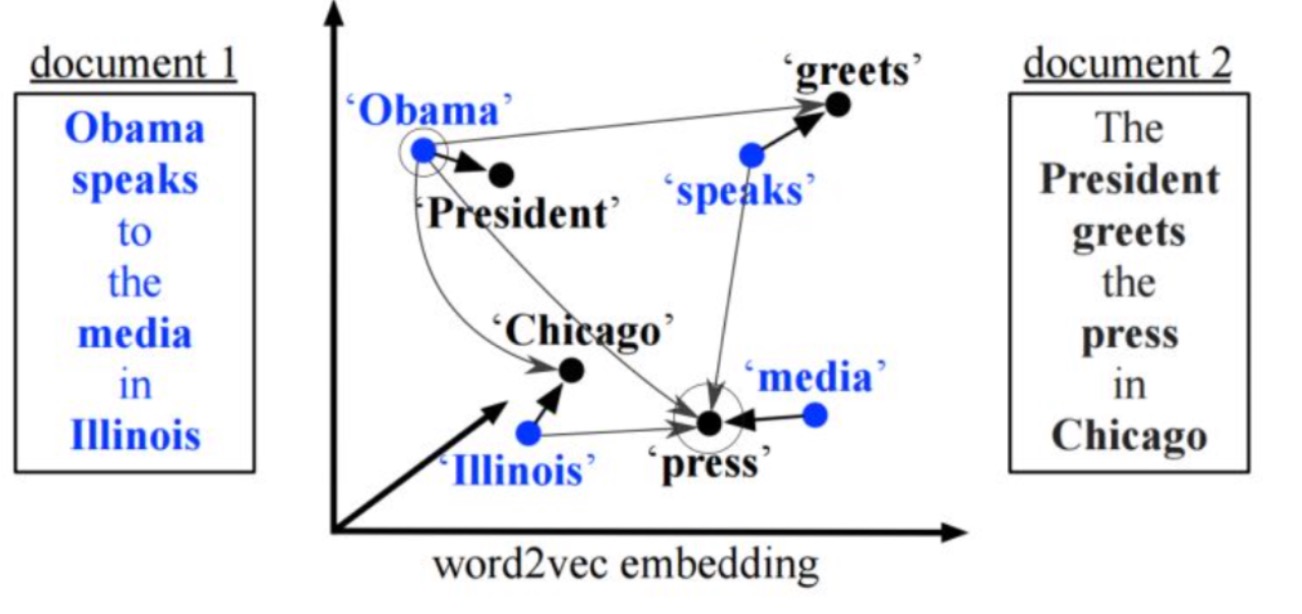： 现有两个文档：

document1: Obama speaks to the media in Illinois. document2: The president greets the press in Chicago.

经过去停用词等预处理之后，两文档分别剩下了四个黑体词。两个文档表示同一个意思，但是如果使用 bag-of-words 或者 tf-idf，是无法表达的。图中 文档1 中的蓝色黑体词与 文档2 中的黑色黑体的 embedding 进行匹配，单词之间的距离看做代价，我们要寻找 文档1 中每个单词分配权重和代价之积的加和最小的路径。最终的寻找结果如图：

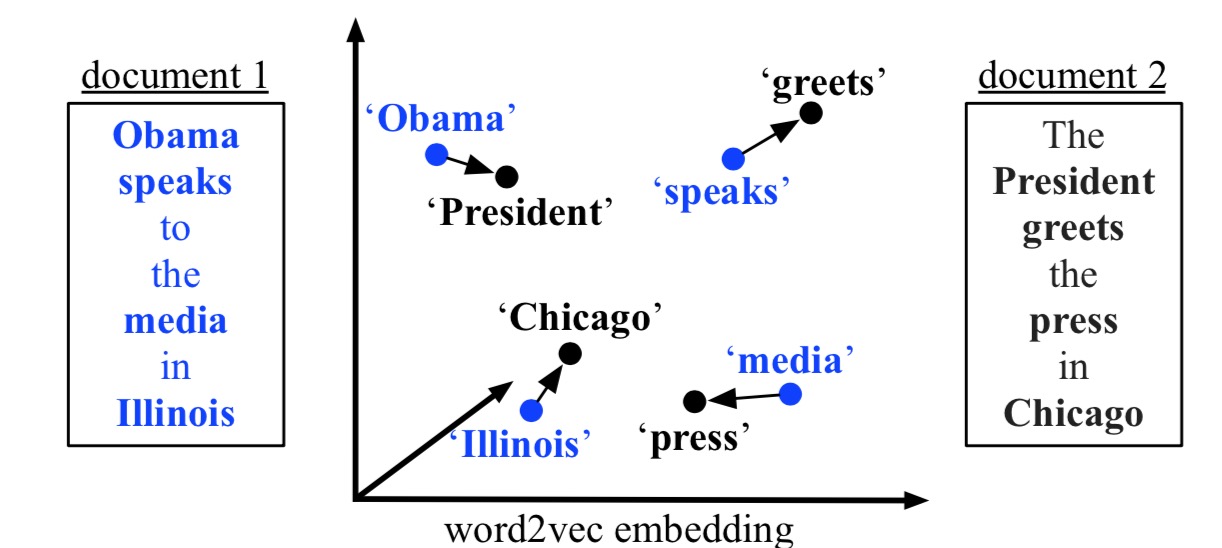
首先将两个文档表示为 nBOW 向量，每个单词的权重定义为 \(d_i = \frac{c_i}{\sum_{j=1}^n{c_j}}\)。然后我们允许 文档1 中的每个单词和 文档2 中的每个单词进行匹配，$T_{ij}$ 表示 文档1 中的 单词i 和 文档2 中的 单词j 之间的转换矩阵，其中$T_{ij} \geq 0$。为了使 文档1 和 文档2 之间完全转化，我们要保证 单词i 中流出的权重之和为$d_i$，并且 单词j 中流入的权重之和为$d{_j}^{‘}$。用公式表示为 \(\sum_{j}{T_{ij}} = d_i\)，\(\sum_{i}{T_{ij}} = d{_j}^{\prime}\)，并且将两个单词之间的距离作为转换代价 c(i,j)，两个文件之间的距离定义为 \(\sum_{i,j}{T_{ij}c(i,j)}\)。

这样，上述问题就完整转化成了一个线性规划问题： \[ min \sum_{i,j=1}^n{T_{ij}c(i,j)} \] subject to: \[ \sum_{j=1}^n{T_{ij}} = d_i \]

\[ \sum_{i=1}^n{T_{ij}} = d{_j}^{\prime} \]

其中 $ i \in { 1, …, n } $, $ j \in { 1, …, n } $。上述问题是前边提到的 EMD 问题的特例，可以求得最优解。但是算法的复杂度为 $ O(p^3logp) $ ，p表示文档1中有而文档2中没有的单词个数。

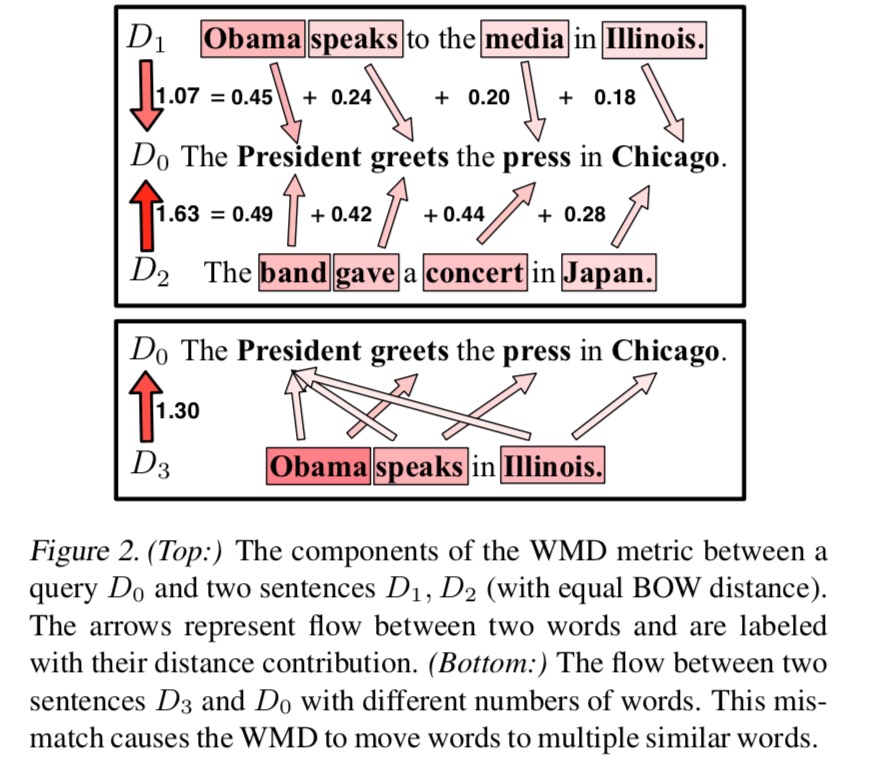
上图是计算文档间距离的一个示例。上边表示，文档 $D_1$ 和文档 $D_2$ 与文档 $D_0$ 之间的计算方法。文档 $D_1$ 中每个单词分配的权重为 $d_i=0.25$。下图中文档 $D_3$ 中每个单词分配的权重为 $d_i=0.33$，值得注意的是，$D_3$ 和 $D_0$ 中匹配时个数并不相等。

优化

WMD算法复杂度如此之高，如何才能快速计算，作者提出了两种优化方式，寻找下界和relaxed WMD。

Word centroid distance

文章通过公式推导，得到一个叫 Word Centroid Distance (WCD) 的距离。具体推导如下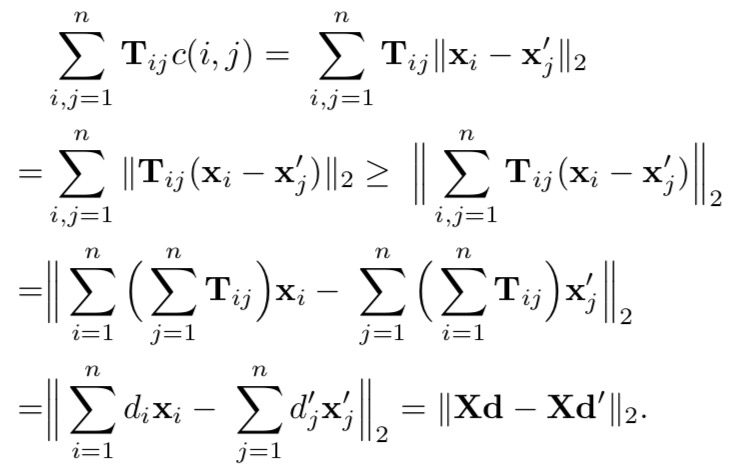： 计算 WCD 的时间复杂度为 $ O(dp) $，大大简化了计算复杂度。我们可以使用 WCD 限制 KNN，在更小的候选子集中进行查找。

Relaxed word moving distance

尽管 WCD 计算很快，但它还不是一个很接近最优的下界。文章中通过分别移除两个限制条件中的一个，来得到更 tighter 的边界。对于这种 relax problem，必然会产生一个比WMD更低的边界，而且如果一个条件被移除，每个WMD问题都会保留一个可行解。

\(\begin{equation} T_{ij}{^*} = \begin{cases} d_i, & \text{if } j = argmin_jc(i,j); \\ 0, & \text{otherwise } x . \end{cases} \end{equation}\) 优化最佳的解决方案就是将d中每个单词的可能性转移到与 $d^\prime$ 中最相似的单词上。上式表现为，如果 j 等于是 c(i, j) 中最小值中的 j，那么最优解为 $d_i$。转化为运输问题可以解释为：如果工厂i和所有仓库的距离中最短的为 仓库j，那么就把 工厂i 中的所有货物都运送到 仓库j 中。

文档D 中的每个词都要找到和文档 $D^\prime$ 中最相似的单词，我们只需要计算 word2vec空间 中单词的欧几里得距离。任意去掉一个限制条件得到每个下界，都依赖于词向量对之间的距离计算。这些距离计算可以组合并重复使用来减少额外开销。我们称得到的最优边界为 Relaxed WMD（RWMD）。复杂度为 $O(p^2)$,计算公式如下： \[ l_r(d, d^\prime) = max(l_1(d, d^\prime), l_2(d, d^\prime)) \]

使用上述优化算法的过程：

先将所有的文档计算 WCD距离，并 降序 排列。取前 K 个文档，计算 WMD 距离。对于剩余文档，先检查是否超过了前 K 个文档的 RWCD下界。如果超过，则将其排除，如果没有，计算 WMD距离。以为 RWCD 是很tigh的，它可以帮助我们排除 95% 的文档，因为节省了大量计算。

另外作者在 NIPS 2016上的后续工作 Supervised Word Mover’s Distance。

参考文献

《From Word Embeddings To Document Distances》 https://en.wikipedia.org/wiki/Earth_mover%27s_distance http://papers.nips.cc/paper/6139-supervised-word-movers-distance