目录：
时间时序，也就是按相等的时间采样的数据点构成的序列轨迹(trajectory)
时间序列数据用于描述现象随时间发展变化的特征。
相似性搜索任务是给定一个时序查询Q，然后从一个时序数据库中返回与Q最相似的时序。
我们使用有序列表来表示一个时间序列 $ T = t_1,t_2,…,t_m $。源数据是一个很长的时间序列，我们最终希望这它的子序列与其进行比较，于是定义子序列为：$ T_{i,k} = t_i,t_i+1,…,t_{i+k-1},其中1 \leq i \leq m-k+1 $。文章中将匹配的子序列 $ T_{i,k} $ 看做C，将要匹配的查询语句定义为Q。计算查询语句和子序列之间的匹配程度，选择使用欧几里得距离（The Euclidean distance (ED)）计算公式如下：
\[
ED(Q,C) = \sqrt{\sum_{i=1}^n{(q_i - c_i)}^2}
\]
上图的阴影部分就是需要计算的欧几里得距离。那么问题来了，如果用两段不同人的语音进行比较，两段语音因为说话速度的不同，停顿时间的不同，音频的峰值会出现不同程度的偏移，如果这时还是用欧几里得距离，会出现计算误差，不能够比较真正程度上的相似性。为了解决这种时间纬度上的不一致性，我们使用DTW的方法，使不同时间点的序列值进行对齐操作。
DTW通过把时间序列进行延伸和缩短，来计算两个时间序列性之间的相似性，如下图所示：
上下两条实线代表两个时间序列，时间序列之间的虚线代表两个时间序列之间的相似的点。DTW使用所有这些相似点之间的距离的和，称之为归整路径距离(Warp Path Distance)来衡量两个时间序列之间的相似性。
在孤立词语音识别中，最为简单有效的方法是采用DTW（Dynamic Time Warping，动态时间归整）算法，该算法基于动态规划（DP）的思想，解决了发音长短不一的模板匹配问题，是语音识别中出现较早、较为经典的一种算法，用于孤立词识别。HMM算法在训练阶段需要提供大量的语音数据，通过反复计算才能得到模型参数，而DTW算法的训练中几乎不需要额外的计算。所以在孤立词语音识别中，DTW算法仍然得到广泛的应用。
DTW的实质是将两个序列的对齐问题转化为二维平面中最优路径的问题。图中，横纵坐标分别表示两个序列，通过对齐操作我们可以绘制出最优路径。路径的选择是一个动态规划的问题。坐标轴的创建和最优路径的查找我们会有规定的限制条件（Constrainsts），以便可以找到最优的路径。
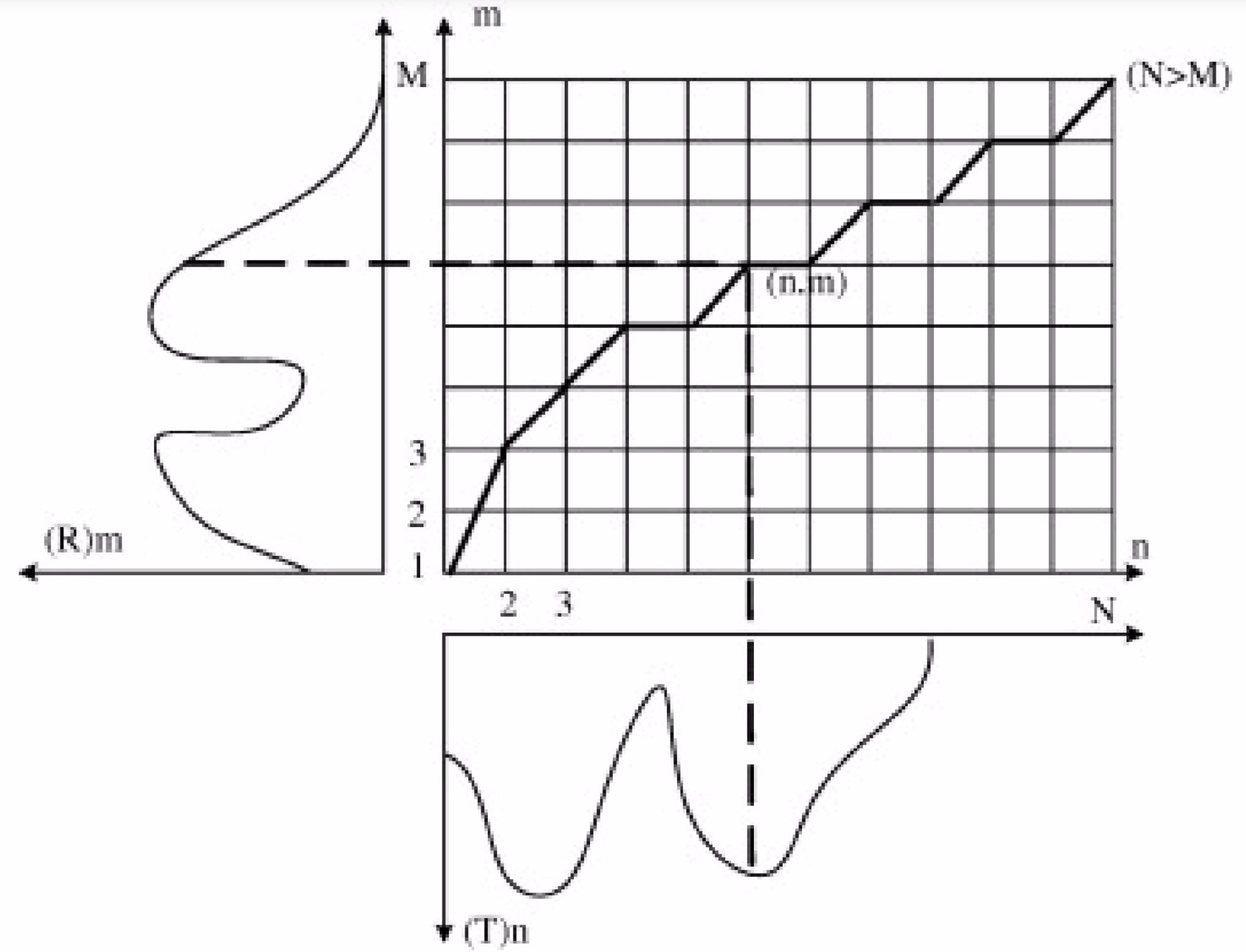
具体限制条件（Constrainsts）如下：
strart，end constraint 第一个限制条件是起始点的限制。当将两个序列对应到二位坐标时，起点的连线要求和原点对应，终点的连线为两序列末端的连线，这样就将问题转化为了二维平面上起点到终点的最优路径问题。
图中要到达（m，n）点可以有多重路径的选择，不如（m-1，n），（m，n-1），（m-1，n-1），（m-2，n），（m，n-2）。这些不同的路劲对应着不同的 Alignment。local constrainst 就是限制每步前进的映射关系。
global constrainst 这个限制条件的意思是在作 Alignment 的时候我们不希望他的跨度太大，比如$T_1$序列中的一个序列点和$T_2$序列中的十个或者更多的序列点对应，这是我们不希望看到的。对应带二维平面上，就是两坐标轴的左边差值要在一个阈值之内，即$|i - j |\leq Threshold $。
weight constrainst 该限制条件是根据实际情况，我们可以为每条路径设置不同的权重。比如在 local constrainst 的图中，我们可以将（m-2，n），（m，n-2）到达（m，n）的权重设置为（m-1，n），（m，n-1），（m-1，n-1）到达（m，n）权重的二倍。这么设置背后的含义是希望能够找到更近的对齐点。
值得注意的是使用
DTW算法的复杂度要比使用欧几里得距离的复杂度高很多，那为什么要使用DTW呢？原因上边有提到，由于使用欧几里得距离计算会因为两个序列在时间维度的偏差而导致错误的匹配结果，比如两个说话速度不同但内容相同的音频，如果使用欧几里得距离计算他们的距离差距很大，然而使用对齐后的DTW计算，会精准地将两个音频作出匹配。问题又来了，DTW复杂度太高，导致我们无法用在实时监控，手势识别领域，如何作出合理的优化是这篇文章的重点所在。
代码整体使用了动态规划的思路。下面是一个使用动态规划计算两点之间最优路径的图。
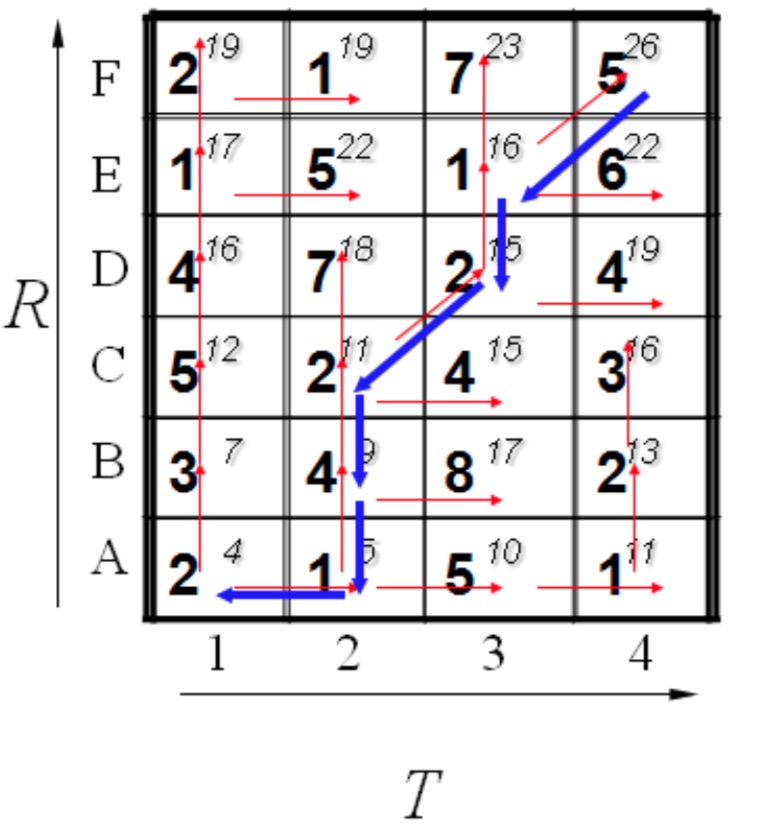代码要点：
euc_dist函数定义了距离的计算方式，这里可以根据需求进行更改。
for j in range(max(1, i- 10), min(n, i+10))循环的范围展示了 global constrainst，规定了对齐序列点的跨度不能大于10。
2*cost+dtw[i-1,j-1]权重的设置这里简单的使用了最短距离权重的倍数的方式，是weight constrainst的体现。
3*cost + dtw[i-1,j-2] if j>1 else sys.maxsize权重设置中的判断体现了 local constrainst。
初始化的过程体现了strart，end constraint。
import numpy as np
import sys
# 定义距离
def euc_dist(v1, v2):
return np.abs(v1-v2)
# DTW的核心过程，实现动态规划
def dtw(s, t):
# s: source sequence
# t: target sequence
m, n = len(s), len(t)
dtw = np.zeros((m, n))
dtw.fill(sys.maxsize)
# 初始化过程
dtw[0,0] = euc_dist(s[0], t[0])
for i in range (1,m):
dtw[i,0] = dtw[i-1,0] + euc_dist(s[i], t[0])
for i in range (1,n):
dtw[0,i] = dtw[0,i-1] + euc_dist(s[0], t[i])
# 核心动态规划流程，此动态规划的过程依赖于上面的图
for i in range(1, m): # dp[][]
for j in range(max(1, i- 10), min(n, i+10)):
cost = euc_dist(s[i], t[j])
ds = []
ds.append(cost+dtw[i-1, j])
ds.append(cost+dtw[i,j-1])
ds.append(2*cost+dtw[i-1,j-1])
ds.append(3*cost + dtw[i-1,j-2] if j>1 else sys.maxsize)
ds.append(3*cost+dtw[i-2,j-1] if i>2 else sys.maxsize)
# pointer
dtw[i,j] = min(ds)
return dtw[m-1, n-1]
文章提到了在万亿级别的时间序列下使用动态时间规整（DTW）的方法进行相似性查询的优化方法。万亿级别的时间序列是个什么概念？文章在开始对这个数字规模进行了详细的说明，之前文献中用到的最大数据集为一亿，万亿的时间序列的规模比之前发表文献中使用的数据集的加和还多。文章提出的的DTW优化后的算法属于精确搜索算法(exact DTW sequential search)，所有的近似搜索算法（approximate search）快得多，更不用说索引搜索方法（在万亿级别的数据上加索引，显然是不现实的）。文章中提到了论文发表之前，关于DTW的几种优化方法，之后又提出了自己的优化方法组件The UCR Suite。通过这些优化方法，可以在相似性搜索中削减99.9999%的DTW计算，速度更快可想而知。
Using the Squared Distance
不管是计算DTW，还是计算欧几里得距离（ED），我们都需要实现对一直结果开根号的非必要操作，开根号是一个既消耗时间又消耗计算机性能工作。其实，对结果不开根号不会改变时间序列与查询序列进行最近邻排序的结果。所以这个才做是没有必要的，论文指出，只在代码中使用不开平方根的操作进行计算，最终向用户提供搜索结果。文章中的DTW和ED可以认为是指它们的平方版本。
Lower Bounding(LB)
用来加速像DTW这种具有很高复杂度的序列搜索的一个经典技巧是使用好计算的下界（LB）来删掉没有希望的候选项。
如上图所示，左图表示 $LB_{Kim}$ 下界，右图为使用了 $LB_{Keogh}$ 下界。$LB_{Keogh}$ 下界计算了候选子序列C和它的包络{U,L}之间欧几里得距离。
《Evaluation of Lower Bounding Methods of Dynamic Time Warping (DTW)》这篇论文中对比了几种边界的好坏，我们简述本篇文章中使用的两种边界。
$LB_{Kim}$下界 作者从查询序列和对比序列中提取了四种特征：即两个序列中的第一个序列点的差异、最后一个序列点的差异、取最大值的序列点的差异和取最小值的序列点之间的差异。如下图所示：
四个特征中的最大值为最小边界距离，所取的最小边界就是 $LB_{Kim}$ 下界。
$LB_{Keogh}$下界 这是一种精确的下界，它形成了对查询序列的一个包络线 {U, L}。最低下界就是查询序列的上的包络与数据序列中的元素之间的平方差之和的平方根，也是查询序列的最小包络与数据序列中的元素之间的平方差之和的平方根。
该篇论文指出，Keogh等人开创了一个使用包络线的下界测量的新时代。在$LB_{Keogh}$之后，几乎所有其他的下边界测量都使用了包络。
作者这里对原始的 $LB_{Kim}$ 下界进行了改进，由于 $LB_{Kim}$ 下界需要计算四个特征，导致计算的复杂度为o(n)。但是经过归一化后的，最大值和最小值之间的差距是很小的，额外计算他们并不合算。所以这里使用起始点的距离，作为 $LB_{Kim}$ 下界，这样时间复杂度就变成了o(1)。
Early Abandoning of ED and LB_Keogh
在计算欧几里得距离或 $LB_{Keogh}$ 下界的过程中，如果我们注意到每对对应数据点之间的平方差之和超过了目前为止的最佳值，那么我们就可以停止计算，确保已知的精确距离或更低，如果我们计算的话，更新后的最佳值会超过迄今为止的最佳值，如图下图所示。
Early Abandoning of DTW
由于 $LB_{Keogh}$ 下界的计算属于近似计算，如果我们计算出来完整的 $LB_{Keogh}$ 下界，那么我们需要进行更精确的 DTW 计算，我们可以使用这个技巧。如下图所示，我们从左到右计算 DTW。
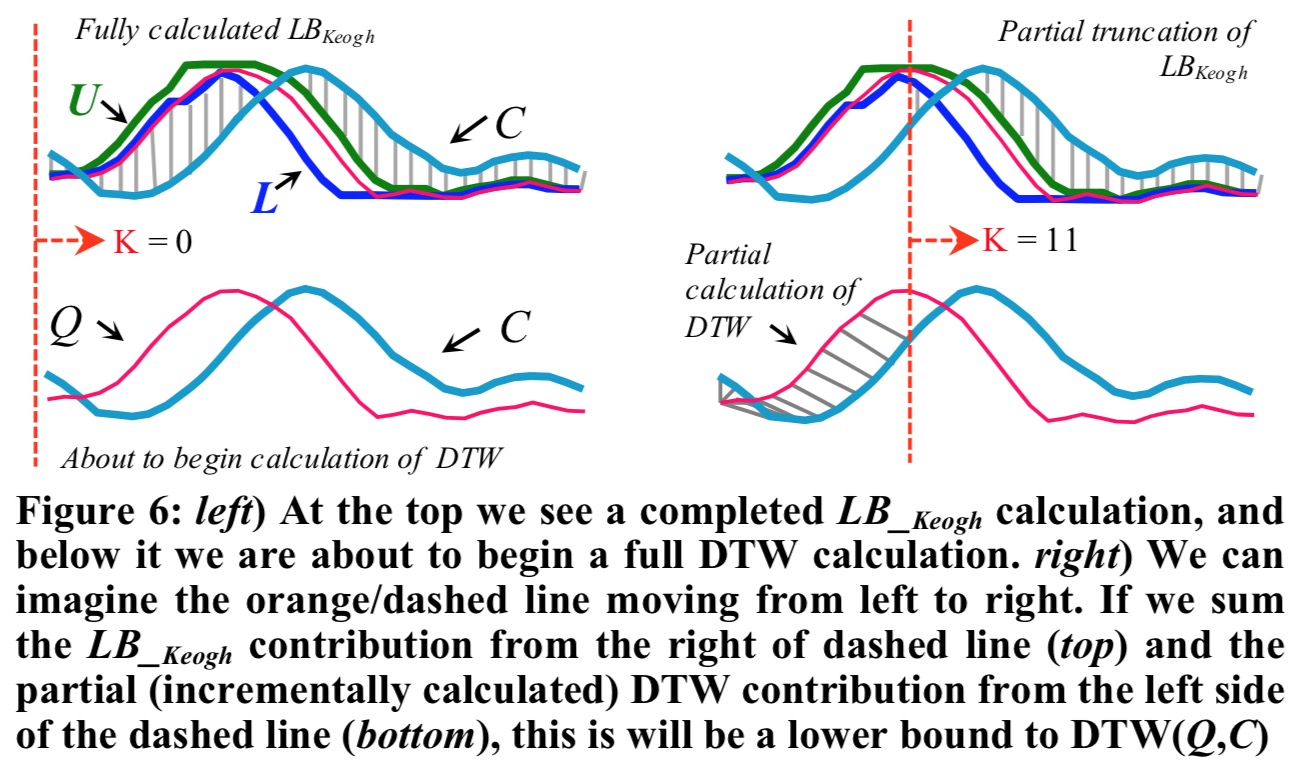从 1 到 K 计算 DTW，我们可以到 1 到 K 的 DTW 贡献值和 K+1 到 n 的 $LB_{Keogh}$ 贡献值，用公式表示为： $ DTW(Q_{1:K},C_{1:K}) + LB_{Keogh}(Q_{K+1:n},C_{K+1:n}) $ 。上式计算的 DTW 边界比实际的 DTW 距离（$ DTW(Q_{1:n},C_{1:n}) $）要低。如果我们在任何时候计算的 $ DTW(Q_{1:K},C_{1:K}) + LB_{Keogh}(Q_{K+1:n},C_{K+1:n}) $ 超出了最佳距离，我们就可以提前结束该序列 DTW 的计算并删除该序列。
Exploiting Multicores
虽然多核来对相似性比较进行线性加速，但是作者的目标是使用单核在 一秒 不到的时间进行查询序列为 421322 长度的相似性匹配。该任务使用单核进行 DTW 计算耗时 182 分钟，使用八核耗时 23 分钟。
论文将提出来的优化方法简称为 The UCR Suite，具体方法如下：
Early Abandoning Z-Normalization
论文中首先提到了对数据进行Z-normalization 的重要性。对数据进行标准化可以大幅提升匹配的准确度。文章率先提出优化标准化这一步，作者发现标准化比计算欧几里得距离还要耗时。作者的观点是对于每一对点可以将the early abandoning calculations of Euclidean distance (or LB_Keogh) 计算与Z-normalization同时进行。换句话说，当我们递增地计算进行Z-normalization时，我们可以同时递增地计算同一组数据点的 the Euclidean distance (or LB_Keogh) 。如果在标准化阶段就可以抛弃，那么就可以不用进行Early Abandoning of ED and LB_Keogh的步骤。
论文中给出了均值和方差的计算公式，如果想要对数据进行标准化，那么均值和方差是必须要计算出来的，然后使用归一化公式进行标准化。正巧在计算对应序列的欧几里得距离或者 $LB_{Keogh}$ 下界的过程中也涉及均值和方差中的计算过程，那么为了节约计算，在归一化一组序列点后直接计算该组点的欧几里得距离或者 $LB_{Keogh}$ 下界。如果在归一化阶段可以抛弃这组点，那么久没有必要继续计算两个序列的距离，这组序列就可以直接抛弃。
那么什么时候可以放弃归一化呢？根据论文中给出的算法，我觉得是这样的，在进行归一化操作之后，进行 the Euclidean distance (or LB_Keogh) 计算，如果计算的距离值大于最佳值（best-so-far），那么可以停止计算。作者还给出了两个滞留 m 个值的长时间序列的均方差计算公式，此过程用到了归一化的子过程。在计算过程中还使用了一个可循环的缓存区用来存储当前一对序列的比较结果，然而这样做的潜在问题就是会造成误差的累计。所以作者每计算一百万个子序列，就会强制对下一个序列进行完整的Z-normalization操作，来清除这种累计的错误。
Reordering Early Abandoning
在之前的方法中，我们都是从左到右依次进行标准化或者计算距离的，作者对这样的计算顺序提出质疑，并提出了更好的计算顺序，过程感觉类似与田忌赛马。让我们看下图：
这部分作者推测，最优的排序方法是基于对查询序列 Q 标准化后的绝对值进行的。在相似性查询过程中，子序列 $C_i$ 要和 Q 进行比较，而 $C_i$ 进行归一化后普遍服从高斯分布，且均值为零。因此查询语句中距离均值 0 最远的点，也就是 Q 的顶点，对距离的计算贡献最大。
在上图中，从左到右计算，使用ED early abandoning 技巧，总共计算了9次。而从Q的顶点开始计算，到使用ED early abandoning 技巧，总共计算了5次。作者还通过对心电图序列计算欧几里得距离之后，通过列举对距离计算贡献最大的点发现，最优排序与作者的预测排序（对 Q 绝对值的指数排序）进行了比较，发现秩相关为0.999，更加论证了对计算点进行重排的重要性。另外此技巧与 early abandoning Z-normalization 和ED and LB_Keogh 结合使用。
Reversing the Query/Data Role in LB_Keogh
这部分作者使用了 LB_Keogh 的下界计算方法。将原本 LB_Keogh 中对 Q 的包络（envelope）与 C 计算距离的方法转变为对 C 的包络计算与 Q 的距离。
原本使用的是左图中，使用查询序列 Q 周围的包络{L,U}，计算子序列 C 与 {L,U} 之间的距离。作者进行了反转，变为子序列 C 附近的包络{L,U}与 Q 之间的距离计算下界，此方法计算的下界记为 $LB_{Keogh}EC$。值得注意的是 $LB_{Keogh}EQ \ne LB_{Keogh}EC$，并且计算时间是之前的一半。
Cascading Lower Bounds
这部分是多种LB方式的综合使用。
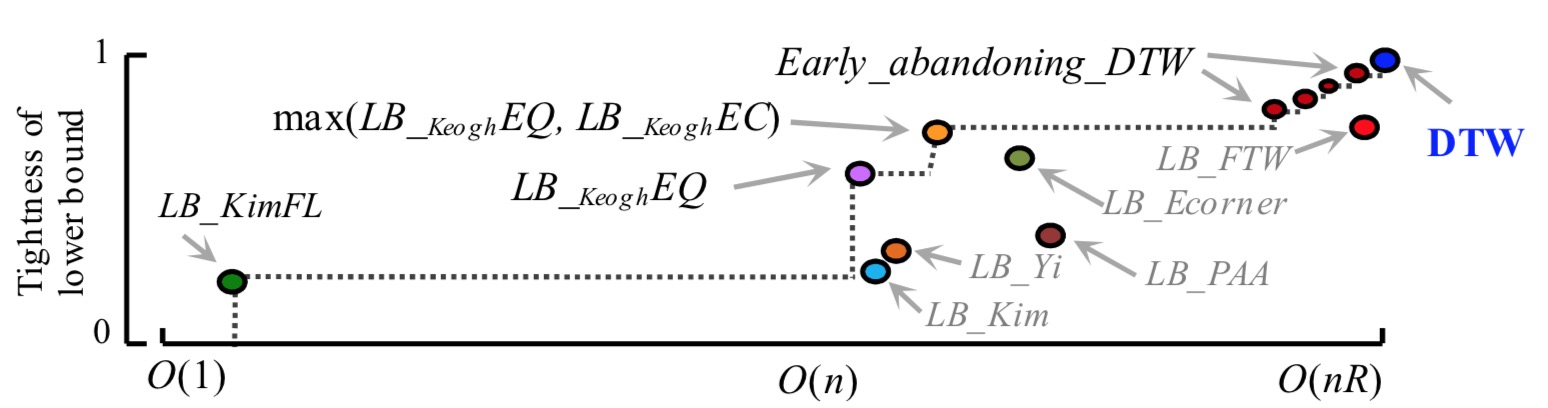如图所示，图中包含了多种下界之间的紧密型与所消耗的时间复杂度。当然，越精确的边界所消耗的时间复杂度越高，画虚线的部分为选取的下界方法，依次使用 $LB_{Kim}FL$，$LB_{Keogh}EQ$， $max(LB_{Keogh}EQ, LB_{Keogh}EC) $，然后使用Early _abandoning_DTW技巧，最后到万不得已在进行 DTW 计算。作者通过实验看到，图中的任何边界都有助于加速计算，删除任何一个边界可能使计算速度慢两倍以上。最后，通过作者提出的 The UCR Suite 优化方法，可以使 DTW 的计算简化 99.9999% 的计算量，大大加快了计算速度。
《Searching and Mining Trillions of Time Series Subsequences under Dynamic Time Warping》
《Evaluation of Lower Bounding Methods of Dynamic Time Warping (DTW)》
论文代码及相关资料：请点击这里 。
