K-Nearest Neighber algorithm

目录：

• K-Nearest Neighber algorithm
  • 一. KNN 算法决策过程
    • 1.1 KNN for Regression (Prediction)
    • 1.2 度量问题
      • 1.2.1 Distance Measure
      • 1.2.2 Edited Measure
  • 二. KNN 的不足
  • 三. KNN 中遇到的问题
    • 3.1 Two Questions

KNN is a non-parameteric model used for classification and regression. The input considts of the K closest training examples in the feature space.

一. KNN 算法决策过程

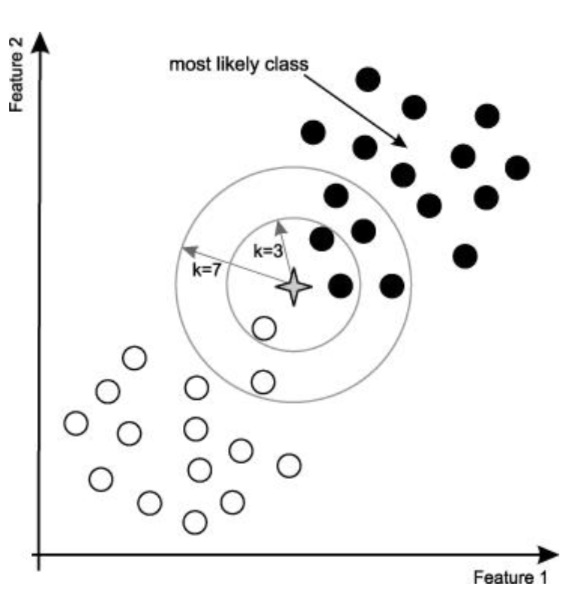
四角星要被决定赋予哪个类，是白色圆圈还是黑色圆圈?
如果 K=3，由于黑色圆圈所占比例为 2/3，四角星将被赋予黑色圆圈那个类。
如果 K=7，由于黑色圈圈比例为 5/7，四角星被赋予黑色与圆圈类。

K 最近邻(k-Nearest Neighbor，KNN)分类算法，是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。该方法的思路是：如果一个样本在特征空间中的 k 个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。KNN 算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。KNN 方法虽然从原理上也依赖于极限定理，但在类别决策时，只与极少量的相邻样本有关。由于 KNN 方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN 方法较其他方法更为适合。KNN 算法不仅可以用于分类，还可以用于回归。通过找出一个样本的 k 个最近邻居， 将这些邻居的属性的平均值赋给该样本，就可以得到该样本的属性。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值(weight)，如权值与距离成正比。

1.1 KNN for Regression (Prediction)

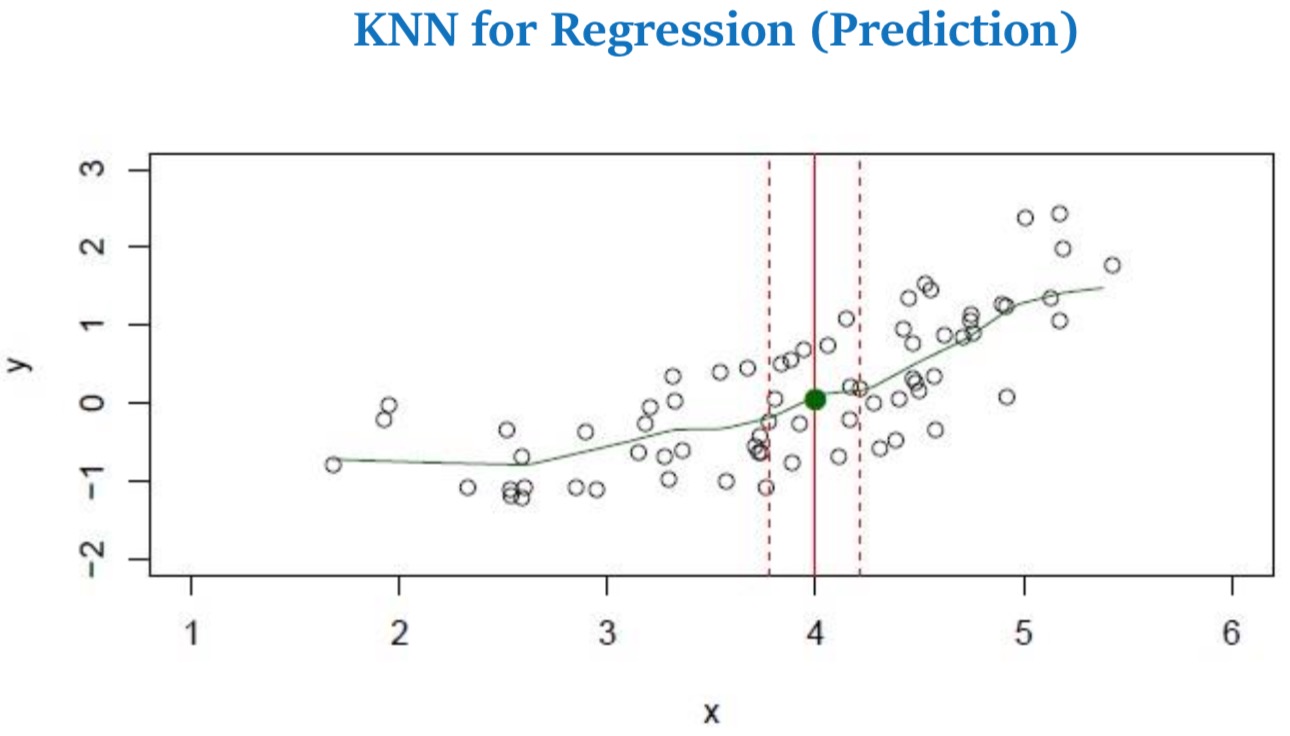
1. Assume a value for the number of nearest neighbors K and a prediction point x0.
2. KNN identifies the training observations No closest to the prediction point x0.
3. KNN estimates f (x0) using the average of all the responses in N0

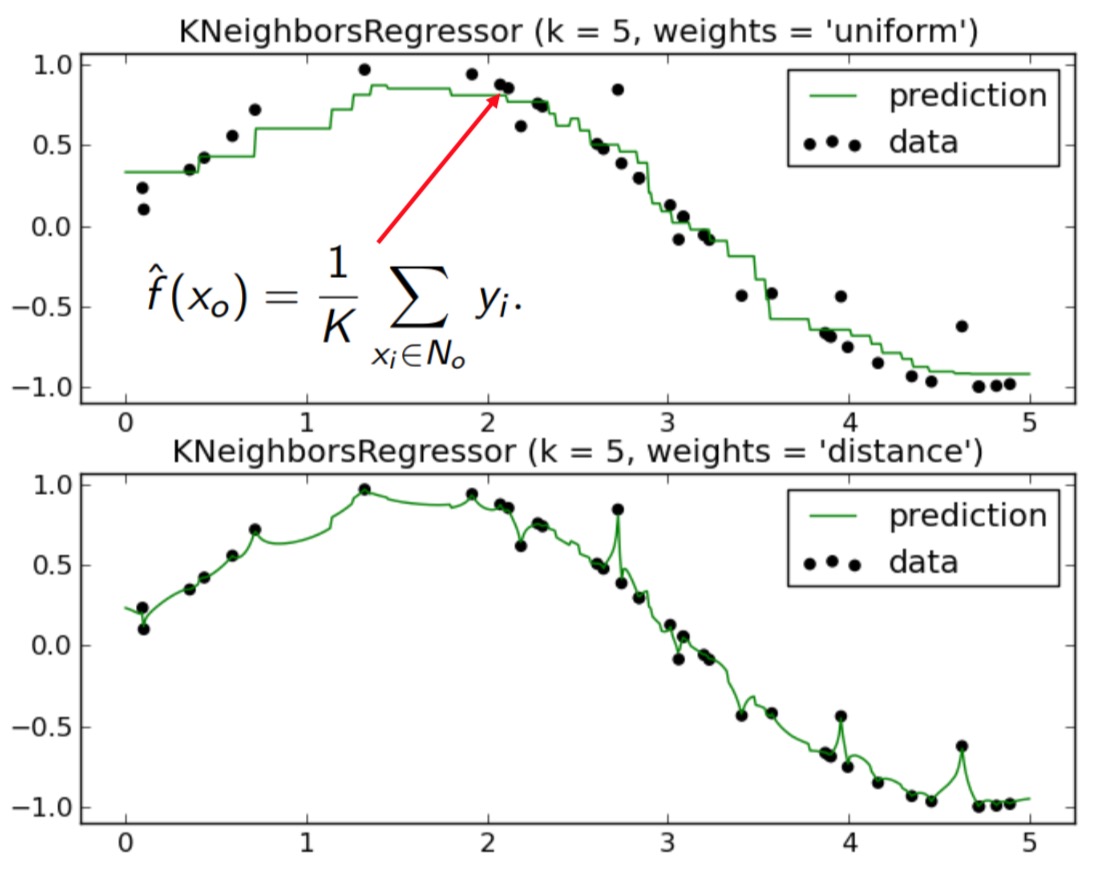
Q: Any better non-parametric model, do we need to adjust the weights? 

1.2 度量问题

1.2.1 Distance Measure

关于距离的度量，两点 A，B 之间的距离d，应该有如下性质：

1. d(A,B) = d(B,A)		symmery(对称性)
2. d(A,A) = 0		    constancy of self-similarity（自相似性的恒定性）
3. d(A,B) = 0   iff	  A = B		positivity separation（分离性）
4. d(A,B) <= d(A,C) + d(B,C)	trangle inquality

以下简单介绍常见的几种距离：

• Euclidean Distance（欧几里得距离）

• Manhattan Distance（曼哈顿距离）

• Minkowski Distance（闵可夫斯基距离)

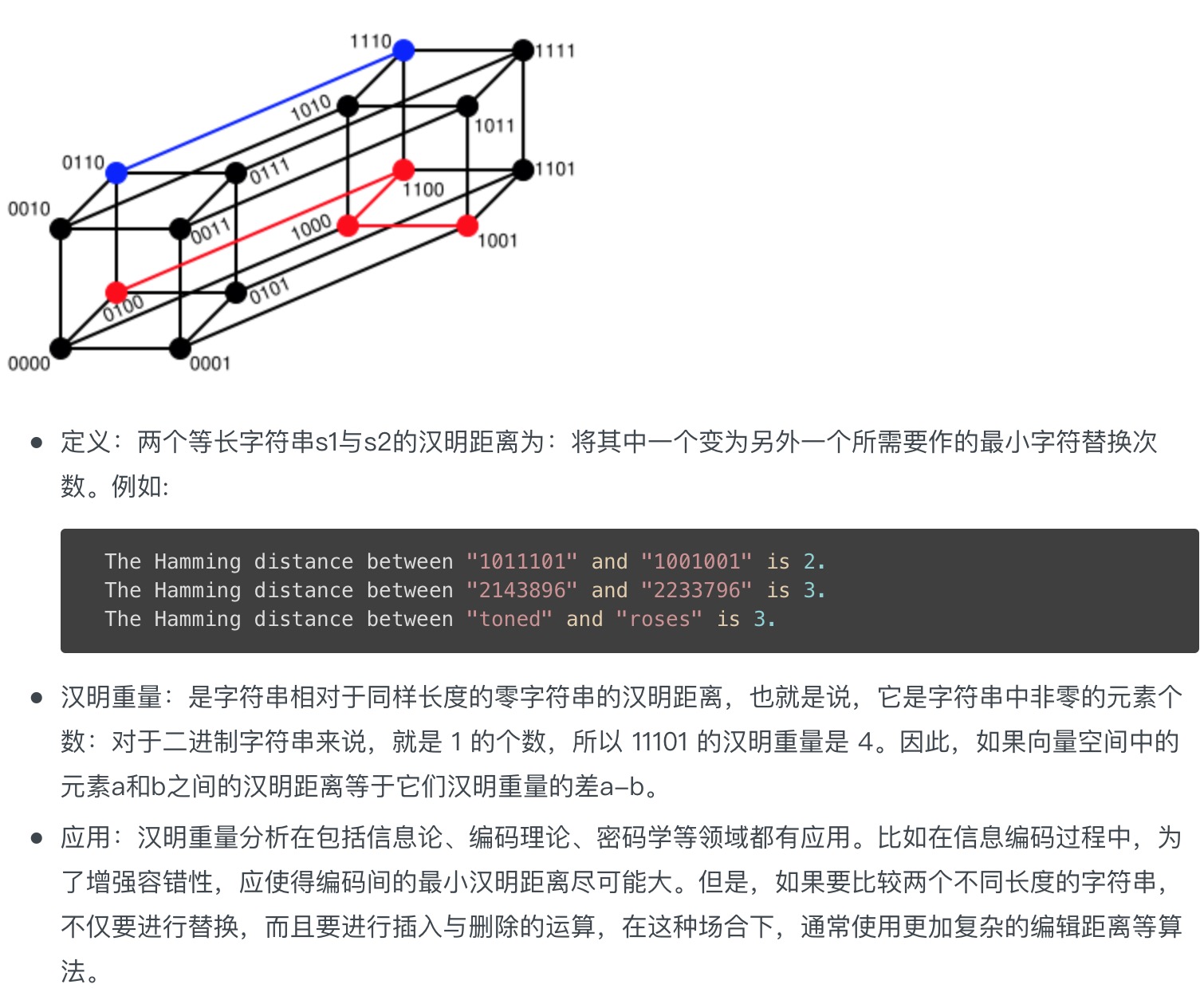
• Hamming Distance（汉明距离）

• Cosine Distance

1.2.2 Edited Measure

To measure the similarity between two objects, transform one into the other, and measure how much effort it took. The measure of effort becomes the distance measure.

给定固定特征，看样本在特征上的表现，关注是否相同。

二. KNN 的不足

• 该算法在分类时有个主要的不足是，当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的 K 个邻居中大容量类的样本占多数。因此可以采用权值的方法(和该样本距离小的邻居权值大)来改进。
• 该方法的另一个不足之处是计算量较大，因为对每一个待分类的文本都要计算它到全体已知样本的距离，才能求得它的 K 个最近邻点。目前常用的解决方法是事先对已知样本点进行剪辑，事先去除对分类作用不大的样本。该算法比较适用于样本容量比较大的类域的自动分类，而那 些样本容量较小的类域采用这种算法比较容易产生误分。

三. KNN 中遇到的问题

3.1 Two Questions

K has to an odd number?

1. KNN for classification:
   如果 K 为偶数，出现的两类别相同，可以根据距离计算离得近的类别，从而进行分类。
   如果 k 为 ∞ 时，只需要看两类的个数。
   如果 k 为 1 时，过拟合。

1. KNN for regression(prediction):
   求 x 对应点处的 y 值，只需将 x 附近取 K 个点，求 K 个点的 y 的平均值即可。另外取K个均值时，由于每个点的贡献不同，可取相应的权重。

What if K becomes very large?

In two dimensions, the nearest-neighbor algorithm leads to a partitioning of the input space into Voronoi cells, each label led by the category of the training point it contains. In three dimensions, the cells are three-dimensional, and the decision boundary resembles the surface of a crystal.

KNN 这部分的代码在另一个仓库中：
<https://github.com/provenclei/tensorflow_learning_path>