目录:
分类技术是机器学习和数据挖掘应用中的重要组成部分。在数据科学中,大约70%的问题属于分类问题。解决分类问题的算法也有很多种,比如:k-近邻算法,使用距离计算来实现分类;决策树,通过构建直观易懂的树来实现分类;朴素贝叶斯,使用概率论构建分类器。这里我们要讲的是Logistic回归,它是一种很常见的用来解决二元分类问题的方法,它主要是通过寻找最优参数来正确地分类原始数据。
逻辑回归(Logistics Regression,简称LR),其实是一个很有误导性的概念,虽然它的名字中带有“回归”两个字,但是它最擅长处理的却是分类问题。LR分类器适用于各项广义上的分类任务,例如:评论信息的正负情感分析(二分类)、用户点击率(二分类)、用户违约信息预测(二分类)、垃圾邮件检测(二分类)、疾病预测(二分类)、 用户等级分类(多分类)等场景。
提到逻辑回归我们不得不提一下线性回归,逻辑回归和线性回归同属于广义线性模型,逻辑回归就是用线性回归模型的预测值去拟合真实标签的对数几率(一个事件的几率(odds)是指该事件发生的概率与不发生的概率之比,如果该事件发生的概率是 P,那么该事件的几率是 $\frac{P}{1-P}$ ,对数几率就是 $log\frac{P}{1-P}$)。
逻辑回归和线性回归本质上都是得到一条直线,不同的是,线性回归的直线是尽可能去拟合输入变量X的分布,使得训练集中所有样本点到直线的距离最短;而逻辑回归的直线是尽可能去拟合决策边界,使得训练集样本中的样本点尽可能分离开。因此,两者的目的是不同的。
我们想要的函数应该是,能接受所有的输入然后预测出类别。例如在二分类的情况下,函数能输出0或1。那拥有这 类性质的函数称为海维赛德阶跃函数(Heaviside step function),又称之为单位阶跃函数(如下图所示):
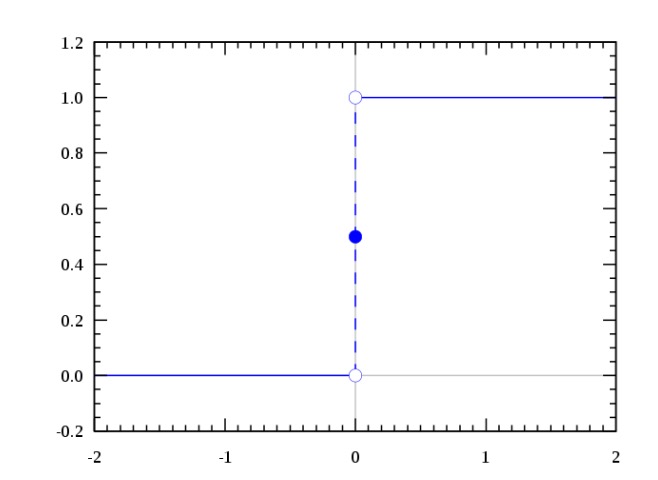
单位阶跃函数的问题在于: 在0点位置该函数从0瞬间跳跃到1,这个瞬间跳跃过程很难处理(不好求导)。幸运的是,Sigmoid函数也有类似的性质,且数学上更容易处理。
Sigmoid函数公式: \(f(x) = \frac{1}{1+e^{-x}}\)
import numpy as np
import math
import matplotlib.pyplot as plt
%matplotlib inline
X = np.linspace(-5,5,200)
y = [1/(1+math.e**(-x)) for x in X]
plt.plot(X,y)
plt.show()
X = np.linspace(-60,60,200)
y = [1/(1+math.e**(-x)) for x in X]
plt.plot(X,y)
plt.show()
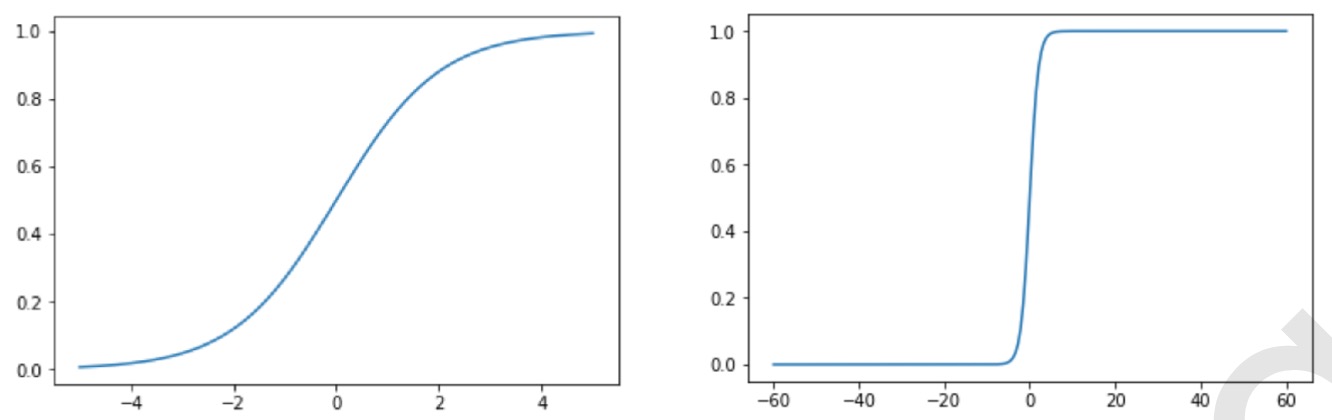
当x为0时,Sigmoid函数值为0.5。随着x的增大,对应的函数值将逼近于1;而随着x的减小,函数值逼近于0。所以Sigmoid函数值域为(0,1),注意这是开区间,它仅无限接近0和1。如果横坐标刻度足够大,Sigmoid函数看起来就很像一个阶跃函数了。
通过将线性模型和Sigmoid函数结合,我们可以得到逻辑回归的公式: \(f(x) = \frac{1}{1+e^{-(\theta^T x+b)}}\) 这样y的取值为(0,1)。对式子进行变换,可得对数几率公式: \(log\frac{y}{1-y} = \theta^T x+b\) 二项 Logistics 回归: \(P(y=0 | x;\theta) = \frac{1}{1+e^{\theta^T x+b}}\) \(P(y=1 | x;\theta) = \frac{e^{\theta^T x+b}}{1+e^{\theta^T x+b}}\)
注意:
- 线性回归和逻辑回归是两类模型,逻辑回归是分类模型,线性回归是回归模型,无可比性。
- 逻辑回归是如何解决多分类问题的呢?二分类问题就是给定的输入 ,判断它的标签是A类还是B类。二分类问题是最简单的分类问题,我们可以把多分类问题转化成一组二分类问题。比如最简单的是OVA(One-vs-all)方法,将一个10分类问题,我们可以分别判断输入x是否属于某个类,从而转换成10个二分类问题。因此,解决了二分类问题,相当于解决了多分类问题。
- 如何用连续的数值去预测离散的标签值呢?线性回归的输出是一个数值,而不是一个标签,显然不能直接解决二分类问题。那我如何改进我们的回归模型来预测标签呢?一个最直观的办法就是设定一个阈值,比如0,如果我们预测的数值 y > 0 ,那么属于标签A,反之属于标签B,采用这种方法的模型又叫做感知机(Perceptron)。另一种方法,我们不去直接预测标签,而是去预测标签为A概率,我们知道概率是一个[0,1]区间的连续数值,那我们的输出的数值就是标签为A的概率。一般的如果标签为A的概率大于0.5,我们就认为它是A类,否则就是B类。这就是逻辑回归模型 (Logistics Regression)。
任何的模型都是有自己的假设,在这个假设下模型才是适用的。
逻辑回归的第一个基本假设是假设数据服从伯努利分布。
\[f(x) = p^x (1-p)^{1-x}\]伯努利分布:是一个离散型概率分布,若成功,则随机变量取值1;若失败,随机变量取值为0。成功概率记为 p,失败为 q = 1-p。
在逻辑回归中,既然假设了数据分布服从伯努利分布,那就存在一个成功和失败,对应二分类问题就是正类和负类,那么就应该有一个样本为正类的概率p,和样本为负类的概率1-p。具体我们写成这样的形式: \(p = h_{\theta}(x;\theta)\)
\[q = 1 - h_{\theta}(x;\theta)\]逻辑回归的第二个假设是正类的概率由 sigmoid 的函数计算,即:
\(p = \frac{1}{1+e^{-(\theta^T x+b)}}\)
预测样本为正类的概率: \(p(y = 1 | x;\theta) = h_{\theta}(x;\theta) = \frac{1}{1+e^{-(\theta^T x+b)}}\) 预测样本为负类的概率: \(p(y = 0 | x;\theta) = 1 - h_{\theta}(x;\theta) = \frac{1}{1+e^{\theta^T x+b}}\) 写在一起,即预测样本的类别: \(\hat{y} = {p(y = 1 | x;\theta)}^y{p(y = 0 | x;\theta)}^{1-y}\) 预测值表示$\hat{y}$,表示预测正类(或者负类)的概率,通常在0~1之间。更具体的过程应该是分别求出正类的概率即y=1时,和负类的概率y=0时,比较哪个大,因为两个加起来是1,所以我们通常默认的是只用求正类概率,只要大于0.5即可归为正类,但这个0.5是人为规定的,如果愿意的话,可以规定为大于0.6才是正类,这样的话就算求出来正类概率是0.55,那也不能预测为正类,应该预测为负类。
逻辑回归的损失函数是它的极大似然函数。
极大似然估计:利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值(模型已定,参数未知)
再联系到逻辑回归里,一步步来分解上面这句话,首先确定一下模型是否已定,模型就是用来预测的那个公式: \(\hat{y} = {(\frac{1}{1+e^{-(\theta^T x+b)}})}^y{(\frac{1}{1+e^{\theta^T x+b}})}^{1-y}\)
参数就是里面的$\theta$ ,x是样本特征,y为标签,我们的已知信息就是在特征取这些值的情况下,它应该属于y类(正或负)。反推最具有可能导致这些样本结果出现的参数,举个例子,我们已经知道了一个样本点,是正类,那么我们把它丢入这个模型后,它预测的结果一定得是正类,才是我们所期望的,我们要尽可能的让上式最大,这样才符合我们的真实标签。反过来一样的,如果你丢的是负类,那这个式子计算的就是负类的概率,同样我们要让它最大,所以此时不用区分正负类。
一直只提了一个样本,但对于整个训练集,我们当然是期望所有样本的概率都达到最大,也就是我们的目标函数,本身是个联合概率,但是假设每个样本独立,那所有样本的概率就可以写成:
\[f(\hat{y}) = \frac{1}{N}\prod_{i=1}^N{(\frac{1}{1+e^{-(\theta^T x_i+b)}})}^{y_i}{(\frac{1}{1+e^{\theta^T x_i+b}})}^{1-y_i}\]此时,只能叫它目标函数,如何对目标进行优化,就是极大似然的纠结过程,那损失函数是啥呢?一般别的算法里,损失函数都是真实值和预测值的误差确定的。而对于逻辑回归,损失函数就是最终极大似然求解公式的负数,所以它也叫log损失。
下边是又极大似然得到log损失的过程:
第一步,取对数,去掉连乘,变为连加,直接给出化简后的结果: \(log(f(\hat{y})) = \frac{1}{N}\sum_{i=1}^N{({y_i}log(\frac{1}{1+e^{-(\theta^T x_i+b)}})}+{(1-y_i)}{log(\frac{1}{1+e^{\theta^T x_i+b}}))}\) 第二步,最大似然和最小化损失函数恰好相反,为了迎合一般要最小化损失函数,所以加个负号: \(-log(f(\hat{y})) = -\frac{1}{N}\sum_{i=1}^N{({y_i}log(\frac{1}{1+e^{-(\theta^T x_i+b)}})}+{(1-y_i)}{log(\frac{1}{1+e^{\theta^T x_i+b}}))}\) 第三步,化简之后就可以称为损失函数了: \(loss = -\frac{1}{N}\sum_{i=1}^N{({y_i}log(\frac{1}{1+e^{-(\theta^T x_i+b)}})}+{(1-y_i)}{log(\frac{1}{1+e^{\theta^T x_i+b}}))}\)
当损失过于小的时候,也就是模型能够拟合绝大部分的数据,这时候就容易出现过拟合。为了防止过拟合,我们会引入正则化。
简单地讲,L1正则就是在损失函数之后加入参数的L1范数,也称之为拉普拉斯先验,同理,L2正则是在损失函数之后加入参数的L2范数,相当于引入了正态分布的先验。在线性回归的损失函数中加入L1或L2正则,会分别变为Lasso回归和Ridge Regression(岭回归)。请参考参考文献1。 这里简单总结下两种正则的区别:
我们通常使用梯度下降对损失函数进行求解。常见的有如下方法:
不过在使用上述三种方法时有两个问题是不可避免的:
针对以上问题,就提出了诸如Adam,动量法等优化方法,有时间一起总结。
对于梯度下降的算法调优,有以下方面值得考虑:
逻辑回归的可解释性逻辑回归最大的特点就是可解释性很强。在模型训练完成之后,我们获得了一组n维的权重向量 $\theta$ 跟偏差 b。对于权重向量 $\theta$,它的每一个维度的值,代表了这个维度的特征对于最终分类结果的贡献大小。假如这个维度是正,说明这个特征对于结果是有正向的贡献,那么它的值越大,说明这个特征对于分类为正起到的作用越重要。对于偏差b (Bias),一定程度代表了正负两个类别的判定的容易程度。假如b是0,那么正负类别是均匀的。如果b大于0,说明它更容易被分为正类,反之亦然。根据逻辑回归里的权重向量在每个特征上面的大小,就能够对于每个特征的重要程度有一个量化的清楚的认识,这就是为什么说逻辑回归模型有着很强的解释性的原因。
逻辑回归的决策边界是否是线性的?
相当于问下列曲线是不是的线性的:
\(\frac{1}{1+e^{-\theta^{T} x}} = 0.5\)
稍微化简一下上面的曲线公式,得到:
\(-\theta^{T} x = 0\)
我们得到了一个等价的曲线,显然它是一个超平面(它在数据是二维的情况下是一条直线)。

相同点:
| 都是有监督分类方法,判别模型(直接估计y=f(x)或p(y | x)) 。 |
不同点:
针对这两个案例,我在 github 的另一个仓库中用 jupyter notebook 直接进行了讲解,喜欢的朋友点个 start。链接地址:博客:逻辑回归
逻辑回归优点:
逻辑回归缺点:
面试常见问题:
- 损失函数为什么是log损失函数(交叉熵),而不是MSE? 逻辑回归模型预估的是样本属于某个分类的概率,其损失函数(Cost Function)可以像线型回归那样,以均方差来表示;也可以用对数、概率等方法。损失函数本质上是衡量”模型预估值“到“实际值”的距离,选取好的“距离”单位,可以让模型更加准确。线性回归用的就是使用的平方损失函数。相比之下逻辑回归选择使用log距离有以下原因:第一,平方损失函数函数并非是凸的函数,会得到多个局部最优解,好像可以使用海森矩阵的正定型性进行证明,还有待深究。而用对数似然函数得到高阶连续可导凸函数,可以得到最优解。第二,根据参数的初始化,导数值可能很小(想象一下sigmoid函数在输入较大时的梯度)而导致收敛变慢,而训练途中也可能因为该值过小而提早终止训练。第三,是因为对数损失函数更新起来很快,因为只和x,y有关,和sigmoid本身的梯度无关。logloss的梯度如下,当模型输出概率偏离于真实概率时,梯度较大,加快训练速度,当拟合值接近于真实概率时训练速度变缓慢,没有MSE的问题。以下这篇文章讲将两种损失函数进行了对比,讲解比较细致,可以参考参考文献3。
- 逻辑回归在训练的过程当中,如果有很多的特征高度相关或者说有一个特征重复了100遍,会造成怎样的影响? 如果在损失函数最终收敛的情况下,其实就算有很多特征高度相关也不会影响分类器的效果。但是对特征本身来说的话,假设只有一个特征,在不考虑采样的情况下,你现在将它重复100遍。训练完以后,数据还是这么多,但是这个特征本身重复了100遍,实质上将原来的特征分成了100份,每一个特征都是原来特征权重值的百分之一。如果在随机采样的情况下,其实训练收敛完以后,还是可以认为这100个特征和原来那一个特征扮演的效果一样,只是可能中间很多特征的值正负相消了。
- 为什么我们还是会在训练的过程当中将高度相关的特征去掉? 去掉高度相关的特征会让模型的可解释性更好。另外,可以大大提高训练的速度。如果模型当中有很多特征高度相关的话,就算损失函数本身收敛了,但实际上参数是没有收敛的,这样会拉低训练的速度。其次是特征多了,本身就会增大训练的时间。